Leetcode discuss: 94. Binary Tree Inorder Traversal

Here is the link. 

C# | Quick learner | Morris traversal | Space optimal: O(1)

Sept. 6, 2022

Morris traversal | O(N) time, O(1) space | Space optimal

Morris (InOrder) traversal is a tree traversal algorithm that does not employ the use of recursion or a stack. In this traversal, links are created as successors and nodes are printed using these links. Finally, the changes are reverted back to restore the original tree.

10 minutes to review the algorithm
Morris traversal Algorithm

• Initialize the root as the current node curr.
• While curr is not NULL, check if curr has a left child.
• If curr does not have a left child, print curr and update it to point to the node on the right of curr.
• Else, make curr the right child of the rightmost node in curr's left subtree.
• Update curr to this left node.

Illustration | Demo | https://www.educative.io/answers/what-is-morris-traversal
It is a good investment to spend 10 minutes to go over a demo before spending time to read C# solution.

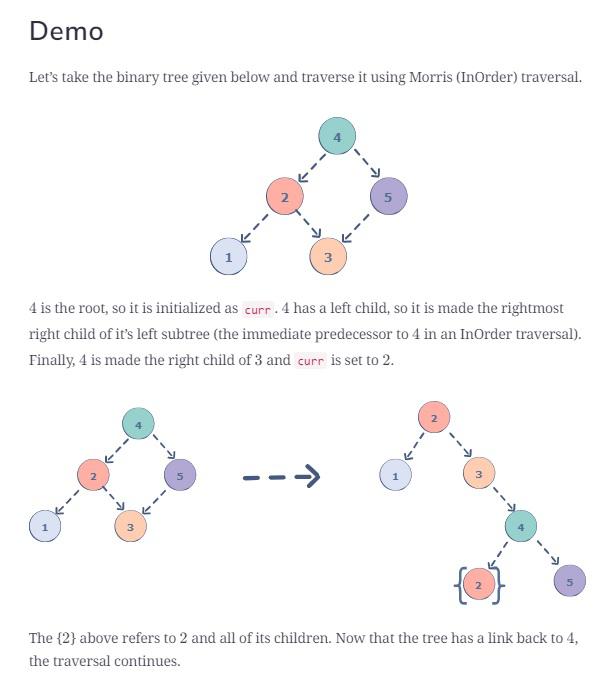
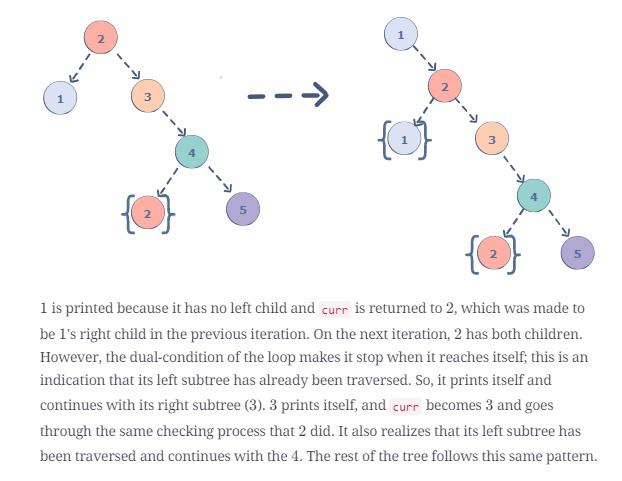
Test cases | Debugging | Tree restored | First node 1 in inorder | Second node 2 in inorder
It is definitely a good exercise to run the debugger, and then track the demo tree first node with value 1 in inorder traversal, and then second node with value 2 in inorder traversal. Rest should be easy. I found out that it is so interesting for me to learn this Morris order traversal with this demo tree.

The following C# code passes online judge.

using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace _94_inorder_traversal
{
    class Program
    {
        public class TreeNode
        {
            public int val;
            public TreeNode left;
            public TreeNode right;
            public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null)
            {
                this.val = val;
                this.left = left;
                this.right = right;
            }
        }

        static void Main(string[] args)
        {
            var root = new TreeNode(4);
            root.left = new TreeNode(2);
            root.right = new TreeNode(5);
            root.left.left = new TreeNode(1);
            root.left.right = new TreeNode(3);            

            var list = InorderTraversal(root);
            Debug.Assert(string.Join(",", list).CompareTo("1,2,3,4,5") == 0);
        }

        /// <summary>
        /// study code
        /// This is C# implementation with Morris In-Order traversal.
        /// Time complexity is O(n)
        /// Space complexity is O(1)
        /// https://leetcode.com/problems/binary-tree-inorder-traversal/discuss/441037/C-Morris-InOrder-Traversal
        /// study Morris traversal
        /// https://www.educative.io/answers/what-is-morris-traversal
        /// Morris (InOrder) traversal is a tree traversal algorithm that does not employ 
        /// the use of recursion or a stack. In this traversal, links are created as successors 
        /// and nodes are printed using these links. Finally, the changes are reverted back to 
        /// restore the original tree.
        /// </summary>
        /// <param name="root"></param>
        /// <returns></returns>
        public static IList<int> InorderTraversal(TreeNode root)
        {           
            var result = new List<int>();

            if (root == null)
            {
                return result;
            }

            var current = root;

            while (current != null)
            {
                if (current.left == null)
                {
                    result.Add(current.val);
                    current = current.right;
                }
                else
                {
                    // make the current node the right child of the rightmost node in curr's left subtree
                    // illustration please the diagram
                    //
                    // find the predec of current
                    var previous = current.left;
                    while (previous.right != null && previous.right != current)
                    {
                        previous = previous.right;
                    }
                
                    if (previous.right == null)
                    {
                        previous.right = current; // node 3.right = node 4
                        current = current.left; // 
                    }
                    else
                    {
                        previous.right = null;
                        result.Add(current.val); // demo tree - first time, node 2 is node 1's right child
                        current = current.right;
                    }
                }
            }
        
            return result;
        }
    }
}