Leetcode algorithm study: 983. Minimum Cost For Tickets

 March 20, 2022

I like to learn from this Google engineer how to solve 10 algorithms. 

This is the first one. 983. Minimum Cost For Tickets

Here is the link.

Two DP solutions with pictures

votrubac48202

January 26, 2019 8:02 PM

44.8K VIEWS

The higher is the bar, the more you're expected to use dynamic programming (DP) during an interview. This technique requires a lot of practice to grasp; if you've mastered the recursion, DP is the next level.

This problem appeared on LeetCode weekly contest #121, and it's a good problem to practice the DP thinking.

Intuition

For each travel day, we can buy a one-day ticket, or use 7-day or 30-day pass as if we would have purchased it 7 or 30 days ago. We need to track rolling costs for at least 30 days back, and use them to pick the cheapest option for the next travel day.

Here, we can use two approaches: track cost for all calendar days, or process only travel days. The first approach is simpler to implement, but it's slower. Since the problem is limited to one calendar year, it does not make much of a difference; for a generalized problem I would recommend the second approach.

1. Track calendar days

We track the minimum cost for all calendar days in dp. For non-travel days, the cost stays the same as for the previous day. For travel days, it's a minimum of yesterday's cost plus single-day ticket, or cost for 8 days ago plus 7-day pass, or cost 31 days ago plus 30-day pass.

int mincostTickets(vector<int>& days, vector<int>& costs) {
  unordered_set<int> travel(begin(days), end(days));
  int dp[366] = {};
  for (int i = 1; i < 366; ++i) {
    if (travel.find(i) == travel.end()) dp[i] = dp[i - 1];
    else dp[i] = min({ dp[i - 1] + costs[0], dp[max(0, i - 7)] + costs[1], dp[max(0, i - 30)] + costs[2]});
  }
  return dp[365];
}

Optimizations

In the previous solution, we store cost for all calendar days. However, since we only look 30 days back, we can just store the cost for last 30 days in a rolling array.

In addition, we can only look at calendar days within our first and last travel dates, as @zengxinhai suggested.

int mincostTickets(vector<int>& days, vector<int>& costs) {
  unordered_set<int> travel(begin(days), end(days));
  int dp[30] = {};
  for (int i = days.front(); i <= days.back(); ++i) {
    if (travel.find(i) == travel.end()) dp[i % 30] = dp[(i - 1) % 30];
    else dp[i % 30] = min({ dp[(i - 1) % 30] + costs[0],
        dp[max(0, i - 7) % 30] + costs[1], dp[max(0, i - 30) % 30] + costs[2] });
  }
  return dp[days.back() % 30];
}

Complexity analysis

• Time Complexity: O(N), where N is the number of calendar days.
• Space Complexity: O(N) or O(31) for the optimized solution. Stricter, it's a maximum duration among all pass types.

2. Track travel days

We track the minimum cost for each travel day. We process only travel days and store {day, cost} for 7-and 30-day passes in the last7 and last30 queues. After a pass 'expires', we remove it from the queue. This way, our queues only contains travel days for the last 7 and 30 days, and the cheapest pass prices are in the front of the queues.

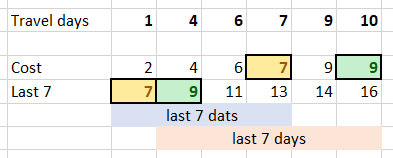
int mincostTickets(vector<int>& days, vector<int>& costs, int cost = 0) {
  queue<pair<int, int>> last7, last30;
  for (auto d : days) {
    while (!last7.empty() && last7.front().first + 7 <= d) last7.pop();
    while (!last30.empty() && last30.front().first + 30 <= d) last30.pop();
    last7.push({ d, cost + costs[1] });
    last30.push({ d, cost + costs[2] });
    cost = min({ cost + costs[0], last7.front().second, last30.front().second });
  }
  return cost;
}

Complexity analysis

• Time Complexity: O(n), where n is the number of travel days.
• Space Complexity: O(38). Stricter, it's a sum of duration for all pass types (1 + 7 + 30 in our case).