1632. Rank Transform of a Matrix

 I like to work on this hard level algorithm. 

Here is the link. 

C# | Quick learner | Union find algorithm | Illustration using diagrams

May 19, 2022
What is the best way to learn this hard algorithm? The algorithm can be solved using Union find algorithm, and then it can be illustrated using a case study by the following diagram:

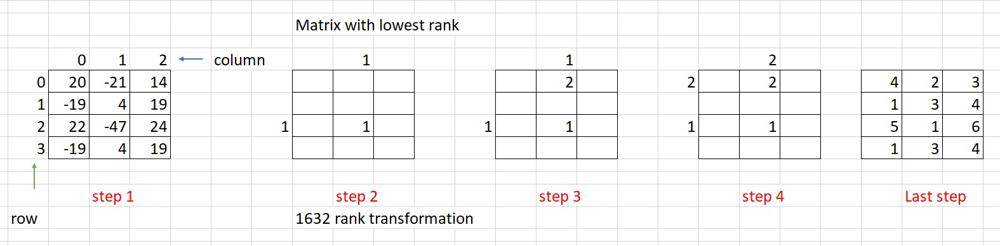
Highlights of my quick learning process:

1. Warmup union find algorithm, disjoint set, ranking, and parent with path compression - Union find algorithm
2. Put every row's items in one disjoint set, and every column's items in one disjoint set;
3. Preprocess a hashmap, so that each root node in disjoint sets can have a list of children nodes
4. Sort all items in matrix by order of value, row number, column number in ascending order.
5. Use extra space to store two integer arrays, rowRanks, colRanks to store latest rank with maximum value.
6. Review the above diagram and study the test case:
7. Smallest value is 47, row = 2, col = 1, set it's rank as 1, and mark rowRanks, colRanks accordingly in second step;
8. Next smallest value is -21, row = 0, col = 1, set it's rank as 2, and mark rowRanks, colRanks accordingly in third step.

Nothing can compare to my own practice | Learn from a failed test case
I did read votrubac analysis but I could not fully understand the idea to solve the problem. I did read a few other discuss post. So I chose to write a C# solution by studying one of C# discuss posts.

I rewrote C# code using more meaningful variable names. I use Tuple<int,int,int> and then I forgot to add a statement in the following:

data.Sort();  // caught by Leetcode online judge

So, I came cross this failed test case, and then I started to debug code using the test case:
3 / 40 test cases passed.
Input:
[[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output:
[[1,2,3],[2,3,4],[3,4,5],[2,3,4]]
Expected:
[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

So it is important to sort all numbers in the matrix first, and then work on smallest value -47.

The following C# code passes online judge.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace _1632_rank_transformation
{
    class Program
    {
        static void Main(string[] args)
        {
            var matrix = new int[3][];
            matrix[0] = new int[] { 20, -21, 14};
            matrix[1] = new int[] { -19, 4, 19};
            matrix[2] = new int[] { 22, -47, 24};
            matrix[3] = new int[] { -19, 4, 19};

            var result = MatrixRankTransform(matrix);
        }

        public class Unions
        {
            private readonly int[] parents;
            private readonly int[] ranks;

            public Unions(int n)
            {
                parents = new int[n];
                ranks = new int[n];
                for (int i = 0; i < n; i++)
                {
                    parents[i] = i;
                }
            }

            public int Find(int x)
            {
                if (x != parents[x])
                {
                    x = Find(parents[x]);
                }

                return parents[x];
            }

            public bool Union(int x, int y)
            {
                int px = Find(x);
                int py = Find(y);

                if (px == py)
                {
                    return false;
                }

                if (ranks[px] > ranks[py])
                {
                    parents[py] = px;
                    ranks[px]++;
                }
                else
                {
                    parents[px] = py;
                    ranks[py]++;
                }

                return true;
            }
        }

        /// <summary>
        /// study code:
        /// https://leetcode.com/problems/rank-transform-of-a-matrix/discuss/909152/Accepted-C-Solution
        /// </summary>
        /// <param name="matrix"></param>
        /// <returns></returns>
        public static int[][] MatrixRankTransform(int[][] matrix)
        {
            var rows = matrix.Length;
            var columns = matrix[0].Length;

            var result = new int[rows][];
            for (int i = 0; i < rows; i++)
            {
                result[i] = new int[columns];
            }

            var disjointSet = new Unions(rows * columns);
            for (int row = 0; row < rows; row++)
            {
                var map = new Dictionary<int, IList<int>>();

                for (int column = 0; column < columns; column++)
                {
                    var current = matrix[row][column];
                    if (!map.ContainsKey(current))
                    {
                        map[current] = new List<int>();
                    }

                    map[current].Add(column);
                }

                foreach (var pair in map)
                {
                    for (int k = 1; k < pair.Value.Count; k++)
                    {
                        disjointSet.Union(row * columns + pair.Value[k], row * columns + pair.Value[k - 1]);
                    }
                }
            }

            // every column - put row's item in a disjoint set. 
            for (int column = 0; column < columns; column++)
            {
                var map = new Dictionary<int, IList<int>>();

                for (int row = 0; row < rows; row++)
                {
                    var val = matrix[row][column];

                    if (!map.ContainsKey(val))
                    {
                        map[val] = new List<int>();
                    }

                    map[val].Add(row);
                }

                foreach (var pair in map)
                {
                    for (int k = 1; k < pair.Value.Count; k++)
                    {
                        disjointSet.Union( pair.Value[k] * columns + column, pair.Value[k - 1] * columns + column);
                    }
                }
            }

            var root2Indices = new Dictionary<int, IList<int>>();
            for (int row = 0; row < rows; row++)
            {
                for (int column = 0; column < columns; column++)
                {
                    var link = row * columns + column;
                    var root = disjointSet.Find(link);

                    if (!root2Indices.ContainsKey(root))
                    {
                        root2Indices[root] = new List<int>();
                    }

                    root2Indices[root].Add(link);
                }
            }

            var data = new List<Tuple<int, int, int>>(rows * columns);

            for (int row = 0; row < rows; row++)
            {
                for (int column = 0; column < columns; column++)
                {
                    data.Add(new Tuple<int, int, int>(matrix[row][column], row, column));
                }
            }

            data.Sort();  // caught by Leetcode online judge

            var rowRanks = new int[rows];
            var colRanks = new int[columns];

            int idx = 0;

            while (idx != rows * columns)
            {
                var tuple = data[idx];
                var row = tuple.Item2;
                var col = tuple.Item3;

                var link = row * columns + col;

                if (result[row][col] != 0)
                {
                    idx++;
                    continue;
                }

                int maxRank = 0;
                var root = disjointSet.Find(link);

                foreach (var index in root2Indices[root])
                {
                    var r = index / columns;
                    var c = index % columns;

                    maxRank = Math.Max(maxRank, Math.Max(rowRanks[r], colRanks[c]));
                }

                var thisRank = maxRank + 1;
                foreach (var index in root2Indices[root])
                {
                    var r = index / columns;
                    var c = index % columns;

                    result[r][c] = thisRank;

                    rowRanks[r] = thisRank;
                    colRanks[c] = thisRank;
                }

                idx++;
            }

            return result;
        }
    }
}