Introduction
It is a hard level algorithm. What I like to do is to learn to write a solution using graph, and then apply BFS algorithm.
Creative idea to construct the graph
Here is my discussion post. I will add more explanation to understand the design.
It is a hard level algorithm. I also like to learn the idea to build a graph using words, and then build a map to contain shortest path to a word.
What I like to practice in 2019 is to push myself to learn a few ideas using graph and also write down some analysis, build strong interest on the algorithm analysis and how to solve a hard level algorithm.
I learn from my own experience to solve this hard level algorithm starting from 2016. I think that it is better to work on a simplified problems similar to word ladder II first. One of problems is to find all paths, not necessary minimimum length. I should learn how to write simple brute force solution, and using backtracking, marking visit efficiently. Here is my practice in Sept., 2019.
This algorithm is a hard level one. What I do is to study one of discussion post in C#, and then I write down my analysis based on my past experience, debugging. I encourage myself to learn a few ideas to solve this hard level algorithm in 2019. This is the first one, without TLE bug.
Case study
I like to write down how to design the graph, and then apply BFS to build a shortest path map, solve the hard level algorithm.
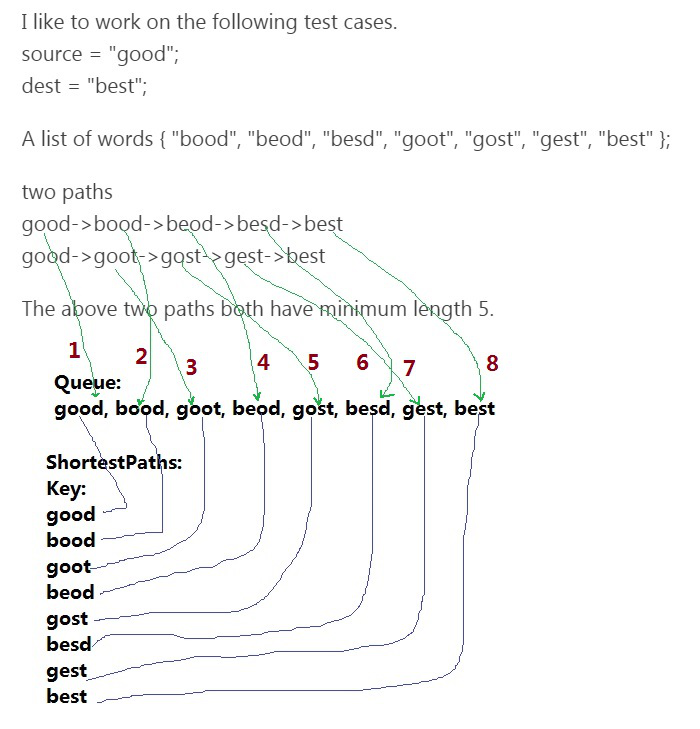
I like to work on the following test cases.
source = "good";
dest = "best";
source = "good";
dest = "best";
A list of words { "bood", "beod", "besd", "goot", "gost", "gest", "best" };
two paths
good->bood->beod->besd->best
good->goot->gost->gest->best
good->bood->beod->besd->best
good->goot->gost->gest->best
The above two paths both have minimum length 5.
More detail
Each word with length 4 has four keys. For example, word "good" can be searched using the following 4 keys:
"*ood"
"g*od"
"go*d"
"goo*".
"*ood"
"g*od"
"go*d"
"goo*".
By going over the start word and all words in dictionary, we can preprocess the graph to build all keys and related words.
For example,
"*ood" can be searched by changing first char to 'a' to 'z', and 'g' and 'b' are in dictionary. So,
"*ood" can be searched by changing first char to 'a' to 'z', and 'g' and 'b' are in dictionary. So,
Key = "*ood"
values = {"good","bood"}.
values = {"good","bood"}.
BFS search more detail
Give the above example, start word from "good", end word is "best", we like to build shorest path from start word to every word encounted in BFS search, first, key is "good", then key is "bood","goot", and so on.
Give the above example, start word from "good", end word is "best", we like to build shorest path from start word to every word encounted in BFS search, first, key is "good", then key is "bood","goot", and so on.
One highlight is to add more entries for same height. We can argue that breadth first search, the first one found should have less and equal value, so new one should just check if it is equal or not.
The above logic is shown in the code. I put comment "reasoning?".
Time complexity
One of my practices ran into time-limit-exceeded error. So it reminds me to pay attention to time complexity, and I find this study code and it should have better time complexity since no timeout.
One of my practices ran into time-limit-exceeded error. So it reminds me to pay attention to time complexity, and I find this study code and it should have better time complexity since no timeout.
All words in dictionary are preprocessed once to build the graph, with special key containing wild char . This makes the algorithm time efficient specially for large amount words in dictionary.
Word dictionary with length = 5 can have maximum words 26^5 = 11,881,376, let us denote using N. So it is important to use algorithm with time complexity O(N), not above O(N).
Here are highlights:
- Understand that it is important to apply BFS search starting from start word in order to find minimum length of path, and also meet the requirement of TLE concern.
- Preprocess the graph first, go over all words in dictionary to build a hashmap, so it will take O(1) to find all one hop away neighbors in the graph.
- Once the end word is visited, terminate the search in the graph. No need to go further to search.
- Design shortest path for each word visited, the path is defined from begin word to any word visited. To allow multiple path with same distance, argue that those visited and found first should have less and equal length.
- C# code using StringBuilder, operator [], good practice compared to using immutable string.
Some art
I do believe that it is a good idea to come out some very good art to present the process of algorithm design. This hard level algorithm is such an interesting algorithm. I like to start to work on the art to illustrate the problem solving starting from selected test cases, two minimum path from good to best, and then draw a queue, show what is order to get into queue, and then shortestPaths are calculated for each key. The shortest path is from "good" to key word.
I will think about more later to make the art of diagram more memorable and helpful for me to learn the problem solving.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _126_word_ladder_II
{
class Program
{
static void Main(string[] args)
{
var source = "good";
var dest = "best";
var words = new string[] { "bood", "beod", "besd", "goot", "gost", "gest", "best" };
var result = FindLadders(source, dest, words);
// two paths
// good->bood->beod->besd->best
// good->goot->gost->gest->best
}
/// <summary>
/// Sept. 9, 2019
/// study code
/// https://leetcode.com/problems/word-ladder-ii/discuss/375730/C-BFS-Solution-faster-than-94-and-less-than-100-memory
/// </summary>
/// <param name="beginWord"></param>
/// <param name="endWord"></param>
/// <param name="wordList"></param>
/// <returns></returns>
public static IList<IList<string>> FindLadders(string beginWord, string endWord, IList<string> wordList)
{
var graph = new Dictionary<string, HashSet<string>>();
preprocessGraph(beginWord, graph);
foreach (var word in wordList)
{
preprocessGraph(word, graph);
}
//Queue For BFS
var queue = new Queue<string>();
//Dictionary to store shortest paths to a word
var shortestPaths = new Dictionary<string, IList<IList<string>>>();
queue.Enqueue(beginWord);
// do not confuse () with {} - fix compiler error
shortestPaths[beginWord] = new List<IList<string>>() { new List<string>() { beginWord } };
var visited = new HashSet<string>();
while (queue.Count > 0)
{
var visit = queue.Dequeue();
//we can terminate loop once we reached the endWord as all paths leads here already visited in previous level
if (visit.Equals(endWord))
{
return shortestPaths[endWord];
}
if (visited.Contains(visit))
continue;
visited.Add(visit);
//Transform word to intermediate words and find matches
// case study: var source = "good";
// go over all keys related to visit = "good" for example,
// keys: "*ood","g*od","go*d","goo*"
for (int i = 0; i < visit.Length; i++)
{
var sb = new StringBuilder(visit);
sb[i] = '*';
var key = sb.ToString();
if (!graph.ContainsKey(key))
{
continue;
}
//brute force all adjacent words
foreach (var neighbor in graph[key])
{
if (visited.Contains(neighbor))
{
continue;
}
//fetch all paths leads current word to generate paths to adjacent/child node
foreach (var path in shortestPaths[visit])
{
var newPath = new List<string>(path);
newPath.Add(neighbor); // path increments one, before it is saved in shortestPaths
if (!shortestPaths.ContainsKey(neighbor))
{
shortestPaths[neighbor] = new List<IList<string>>() { newPath };
} // reasoning ?
else if (shortestPaths[neighbor][0].Count >= newPath.Count) // // we are interested in shortest paths only
{
shortestPaths[neighbor].Add(newPath);
}
}
queue.Enqueue(neighbor);
}
}
}
return new List<IList<string>>();
}
/// <summary>
/// Time complexity is biggest challenge. It is a good idea to use O(N) time to preprocess a graph for the search.
/// How to define the graph? It is kind of creative idea to use wildchar * to replace one char for each word.
///
/// For example word "hit" can be written as "*it", "h*t", "hi*".
/// graph["*it"] = new HashSet<string>{"hit"}
/// graph["h*t"] = new HashSet<string>{"hit"}
/// graph["hi*"] = new HashSet<string>{"hit"}
///
/// git can be written as "*it", "g*t","gi*"
/// so graph["*it"] = new HashSet<string>{"hit","git"}
/// ...
///
/// </summary>
/// <param name="word"></param>
/// <param name="graph"></param>
private static void preprocessGraph(string word, Dictionary<string, HashSet<string>> graph)
{
//For example word hit can be written as *it,h*t,hi*.
//This method genereates a map from each intermediate word to possible words from our wordlist
for (int i = 0; i < word.Length; i++)
{
var sb = new StringBuilder(word);
sb[i] = '*';
var key = sb.ToString();
if (graph.ContainsKey(key))
{
graph[key].Add(word);
}
else
{
var set = new HashSet<string>();
set.Add(word);
graph[key] = set;
}
}
}
}
}
Actionable Items
I reviewed my practice in 2016 on this hard level algorithm. What I did in 2016 is to spend over eight hours, but no submission on this hard level algorithm 126 on Leetcode.com.
It is so surprising for me to learn that back in 2016 I was not so experienced to review and write down my own thought process. I am so glad to see the big difference in 2019 compared to 2016. All blogs are here for me to review my practice in 2016.
No comments:
Post a Comment