April 29, 2021
Here is the link.
C# | optimal time complexity O(N) | post order traversal | bottom up | April 29, 2021
April 29, 2021
- Binary Tree Maximum Path Sum
Introduction
It is tough to perform best when I felt stressed. I rememberd how to write an optimal solution using time complexity O(N) whereas N is total number of nodes. But under stress, I took the approach to call applyPostOrderTraversal() for each node instead of preprocessing and save all node's maximum path sum from root to leaf node, and made it work first. And I noticed that time complexity is O(N^2), and redundant calculation should be avoided.
Optimal solution
I quickly wrote the solution in the following code, and then the code passes online judge. The time complexity is O(N), space complexity is O(N) as well.
Performance challenge
When I design the algorithm, I should consider to apply post order traversal once, and then calculate each node's maximum path sum from root to leaf node. And also it is important to apply preprocess technique, save into C# Dictionary<TreeNode, int>.
It will be very easy to call TreeNode and get it's maximum path sum from root to leaf, and then apply brute force to all nodes in the tree, which is the topest node close to root node in a path.
Time schedule
I do think that it is easy to explain the post order traversal using a few simple tree test case, and explain how it works. It will take me at most five to 10 minutes.
Next it takes me another 5 to 10 minutes to explain idea to apply brute force, maximum path sum cross the root node.
The hard level algorithm should be solved in less than 25 minutes. I should push myself hard to make sure the algorithm is designed with optimal time complexity.
Case study
Given a simple tree like the following, what is maximum path sum:
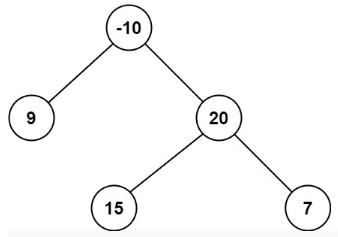
One function call of applyPostOrderTraversal to apply post order traversal, bottom up, root node to leaf node maximum path sum is calculated.
First step is to review post order, the node is visted in the order of a, b, c, d, e.
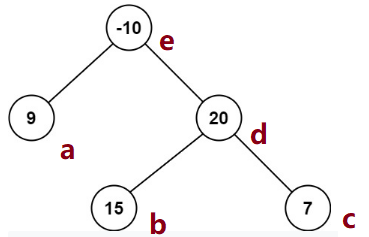
The sum is calculated from root node to leaf node maximum path sum.
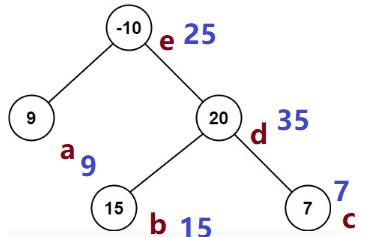
C# Dictionary<TreeNode, int> variable map is populated with the following:
map[TreeNode9] = 9, the path is node 9 itself.
map[TreeNode 15] = 15, the path is node 15 itself.
map[TreeNode 7] = 7, the path is node 7 itself.
map[TreeNode 20] = 35, the path is d-> b
map[TreeNode -10] = 25, the path is e->d->b.
Next step is to go over all nodes in the tree as topest node in the path close to root node, so maximum path sum cross the node is the following:
Node -10: -10 + 35 = 25, the path is e->d->b
Node 9: 9
Node 20: 20 + 15 + 7 = 42, the path is b -> d -> c
Node 15: 15
Node 7: 7
So the maximum path is the one to cross node 20, the maximum path sum is 42.
public class Solution {
public int MaxPathSum(TreeNode root) {
if(root == null)
return 0;
var map = new Dictionary<TreeNode, int>();
applyPostOrderTraversal(root, map);
var crossPathSum = Int32.MinValue;
foreach(var item in map.Keys)
{
var sum = item.val;
if(item.left != null)
{
var left = map[item.left];
if(left > 0)
sum += left;
}
if(item.right != null)
{
var right = map[item.right];
if(right > 0)
sum += right;
}
crossPathSum = Math.Max(crossPathSum, sum);
}
return crossPathSum;
}
private int applyPostOrderTraversal(TreeNode root, Dictionary<TreeNode, int>map)
{
if(root == null)
return 0;
var value = root.val;
var maxRootToLeaf = value;
var left = applyPostOrderTraversal(root.left, map);
var right = applyPostOrderTraversal(root.right, map);
if(left > 0)
{
maxRootToLeaf += left;
}
if(right > 0)
{
maxRootToLeaf = Math.Max(maxRootToLeaf, value + right);
}
map.Add(root, maxRootToLeaf);
return maxRootToLeaf;
}
}






























