Leetcode discuss: 698. Partition to K Equal Sum Subsets

 Here is the link. 

Third practice - C# play with bit manipulation solution

Oct. 29, 2020
698. Partition to K Equal Sum Subsets

It is my 30 minutes learning to write a C# solution to apply bit manipulation. I like to learn the design using a simple test case with the array [1, 2, 3, 4] and k = 2.

Case study
I have to go through the debugging using [1, 2, 3, 4] in order for me to understand the code. But somehow I still am not sure why return dp[n - 1].

size = 2^ 4 = 26
dp[0] = true;
total = new int[16];
In order to save subset sum, let us go over the example,
each number in the array take ith bit as 1.

{1}, first number in the array, take first bit, bit expression: 1 -> integer 1, total[1] = 1, dp[1] = true;
{2}, second number in the array, take second bit, bit expression: 10 -> integer 2, total[2] = 2, dp[2] = true;
{3}, third number in the array, take third bit, bit expression: 100 -> integer 4, total[3] = 3, dp[3] = true;
{4}, fourth number in the array, take fourth bit, bit expression: 1000 -> integer 8, total[8] = 4, dp[8] = true;

if(dp[i]) // in other words, there is a subset in binary format, we can tell what subset it is.
dp[5] - 5 can tell the subset {1, 3}, first bit and third bit is found in 5 { binary format: 101}

Debug result: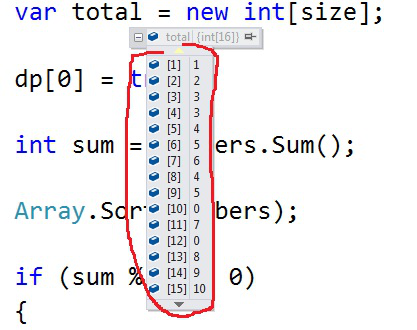

For example, total[6] = 5, subset {2, 3}, total is 5, bit expression for those numbers are 110.
dp[5] = true, in other words, there is a subset to match 5, {2, 3}.

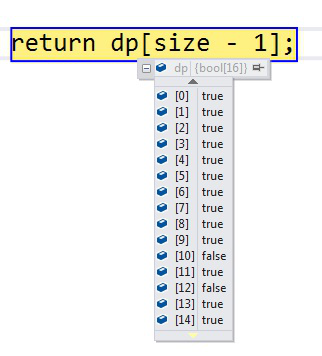
How to understand dp[10] = false, dp[12] = false?
10 -> 1010 -> subset {2, 4}, sum = 6 > 5, so it is not selected. dp[10] = false;
12 -> 1100 -> subset {3, 4}, sum= 7 > 5, sp it is not selected. dp[12] = false;

Advice
It is better for me to go over a simple test case, so that I can learn from my experience. It should be easy for me to come out design next time.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace _698_partition_k_subset___bit
{
    class Program
    {
        static void Main(string[] args)
        {
            var numbers = new int[] { 1, 2, 3, 4 };
            var result = CanPartitionKSubsets(numbers, 2);
        }

        /// <summary>
        /// Oct. 29, 2020
        /// study code
        /// https://leetcode.com/problems/partition-to-k-equal-sum-subsets/discuss/335668/DP-with-Bit-Masking-Solution-%3A-Best-for-Interviews
        /// </summary>
        /// <param name="numbers"></param>
        /// <param name="k"></param>
        /// <returns></returns>
        public static bool CanPartitionKSubsets(int[] numbers, int k)
        {
            if (numbers == null || numbers.Length == 0)
            {
                return false;
            }
		
		    int n = numbers.Length;
		 
            var size = 1 << n; 

            // quick warmup:
            // set A {1,2,3,4,5}
            // the bitmask 01010 represents the subset {2,4}
            // set ith bit:
            // Let i=0, so, (1<<i) = 00001, 01010 | 00001 = 01011
            // unset ith bit:
            // b & !(1<<i)
            // make sure that I understand the above tutorial before I continue to read the code

		    var dp = new bool[size];
		    var total = new int[size];

		    dp[0] = true;
		
		    int sum = numbers.Sum();
		    
		    Array.Sort(numbers);

            if (sum % k != 0)
            {
                return false;
            }

            // continue to use same variable sum -> 1 of k share
		    sum /= k;
            if (numbers[n - 1] > sum)
            {
                return false;
            }

		    // Loop over power set
            for (int i = 0; i < size; i++) 
            {
			    if(dp[i]) 
                {
				    // Loop over each element to find subset
				    for(int j = 0; j < n; j++) 
                    {
					    // set the jth bit - add jth number in the subset
					    int temp = i | (1 << j);
                        var unvisited = temp != i;

                        if (unvisited)
                        {
                            var current = total[i];
                            var jth = numbers[j];
						    // if total sum is less than target store in dp and total array
                            if (jth <= (sum - (current % sum)))
                            {
                                dp[temp] = true;
                                total[temp] = jth + current;
                            }
                            else
                            {
                                break;
                            }
					    }
				    }
			    }
		    }

		    return dp[size - 1];
        }
    }
}