847. Shortest Path Visiting All Nodes | Hard level

June 28, 2022

Here is the link. 

C# | Quick learner | BFS | How to define a state?

June 28, 2022
Introduction
I am approaching 700 algorithms solved mark, but I was still stumbled on this hard level algorithm. It can be prototyped using standard breadth first search algorithm. The challenge part is to avoid dead loop, and how to define unique state in the search.

BFS algorithm | Talk about example graph: Input: graph = [[1,2,3],[0],[0],[0]]
As a quick learner, I was still scared to analyze the graph, how to find the shortest path to visit all nodes in the graph. Given the graph

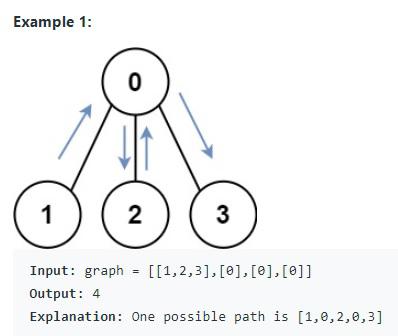
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]
One of shortest path starts from node 1, visit node 0, and then go to node 2, and then go back to node 0, and last go to node 3. All nodes including 0, 1, 2, 3 have been visited. The length of the path is 4, 1->0, 0->2, 2->0, 0->3.

I read a few top-voted discuss posted, and then tried to figure out how to define unique state for BFS in order to avoid deadloop.

The first question is why to visit node 0 twice. How to explain that it is necessary step to visit 0 and go then go to 2 and go back to 0? The node 0 is visited before.

One thing to argue is that in order to visit all nodes, andI can argue that all visited nodes in each step should be unique, otherwise there is a deadloop (? Need to confirm with the following step by step verification. After the verfication, it is not true.).
First step, start from node 1, visited nodes: {}, empty set;
Next step, destination node is 0, visited nodes: {0}, path: 1->0, one unique node;
Next step, destination node is 2, visited nodes: {0, 1}, path: 1->0->2, two unique nodes: {0, 1}
Next step, destination node is 0, visited nodes: {0, 1, 2}, path: 1->0->2->0, three unique nodes: {0, 1, 2}
Last step, destination node is 3, visited nodes: {0, 1, 2}, path: 1->0->2->0->3, there unique nodes: {0, 1, 2 }

So {0, 1, 2} as a sorted set is duplicated twice, first destination is 0, second destination is 3. In order to make it work, I like to argue that state is unique - destination node, unique node id in sorted set <- combination of those two states are unique.

key definition:
Path 1->0->2, {0, 1, 2}, destination 0 => key: 0:0-1-2
Path 1->0->2->0, {0, 1, 2}, destination 3 => key: 3:0-1-2
The above two steps have different key.

By going through the above step by step research, uniqueness definition leads to statesSet variable as a HashSet, the defintion is described in the following statement:

    // graph - at most 12 nodes - Do not care about steps variable's value
    var key = destination.ToString() + ":" + string.Join("-",sortedCopy);

The following C# code passes online judge.

using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace _847_shortest_path
{
    class Program
    {
        static void Main(string[] args)
        {
            var graph = new int[4][];
            graph[0] = new int[] { 1, 2, 3};
            graph[1] = new int[] { 0 };
            graph[2] = new int[] { 0 };
            graph[3] = new int[] { 0 };

            var result = ShortestPathLength(graph);
            // [1, 0, 2, 0, 3]
            Debug.Assert(result == 4);
        }

        /// <summary>
        /// study code
        /// which node we are at & which nodes we've visited
        /// we can make a set of this class to avoid adding duplicate states to the BFS queue (avoid cycles) 
        /// </summary>
        /// <param name="graph"></param>
        /// <returns></returns>
        public static int ShortestPathLength(int[][] graph)
        {
            // Graph node: Number, steps, visited -> mapping to a special key string 
            var statesSet = new HashSet<string>();

            // queue every node into a BFS queue
            // int - number, int - steps, IEnumerable<int> - visited
            // Tuple<int, int, IEnumberable<int>>
            var queue = new Queue<Tuple<int, int, IEnumerable<int>>>();

            // BFS - put all nodes as start point 
            // since we have no idea which node will lead to shortest path
            for (int i = 0; i < graph.Length; i++)
            {
                var visited = new int[] { i };
                queue.Enqueue(new Tuple<int, int, IEnumerable<int>>(i, 0, visited));
            }

            // do BFS until a set is size graph.Length
            while (true)
            {
                int count = queue.Count;

                for (int i = 0; i < count; i++)
                {
                    var current = queue.Dequeue();

                    var number = current.Item1;
                    var steps   = current.Item2;
                    var visited = current.Item3;
                    var sorted = new SortedSet<int>(visited);

                    if (sorted.Count == graph.Length)
                    {
                        return steps;
                    }

                    // For example, graph = [[1,2,3],[0],[0],[0]]
                    // graph[0] has three adjacent edges, [1, 2, 3 ]
                    foreach (int destination in graph[number])
                    {
                        // Make new set by getting popped set and adding new neighbour n
                        var sortedCopy = new SortedSet<int>(visited);
                        sortedCopy.Add(destination);

                        // Make new GraphNode and only add it if it's not a state we've seen before
                        var newNode = new Tuple<int, int, IEnumerable<int>>(destination, steps + 1, sortedCopy);

                        // graph - at most 12 nodes - Do not care about steps variable's value
                        var key = destination.ToString() + ":" + string.Join("-",sortedCopy);

                        if (!statesSet.Contains(key))
                        {
                            queue.Enqueue(newNode);
                            statesSet.Add(key);
                        }
                    }
                }
            }            
        }		    
    }
}