Here is the link.
The post is written by GeorgeChryso. I like to copy and paste the content in the following, and read more carefully and learn a few things.
-Buckle up Jimbo, this one's gonna be a doozy
So, as I found this problem and the variations of its solution rather interesting, I will be explaining every possible approach.
Let's start by the definition of our problem.
However, we can manipulate the data in order to get to easier requirements.
It is now clear, that all I need is to find a combination(subset) of my elements that sums up to the total sum of the array, divided by two.
First comes the easiest approach:
Here's how to implement a simple hashmap where I store every possible combination's sum and a short example:
var canPartition = A => {
let totalSum = A.reduce((acc, curr) => acc + curr);
if (totalSum % 2) return false;
const target = totalSum / 2;
const memo = new Set([0]);
for (let number of A) {
let possibleSums = Array.from(memo);
for (let possibleSum of possibleSums) {
memo.add(possibleSum + number);
}
}
return memo.has(target);
};
BACKTRACKING/DFS
So I deduce that every possible combination is a series of choices for every item-candidate. That is whether to take the item, or ignore it.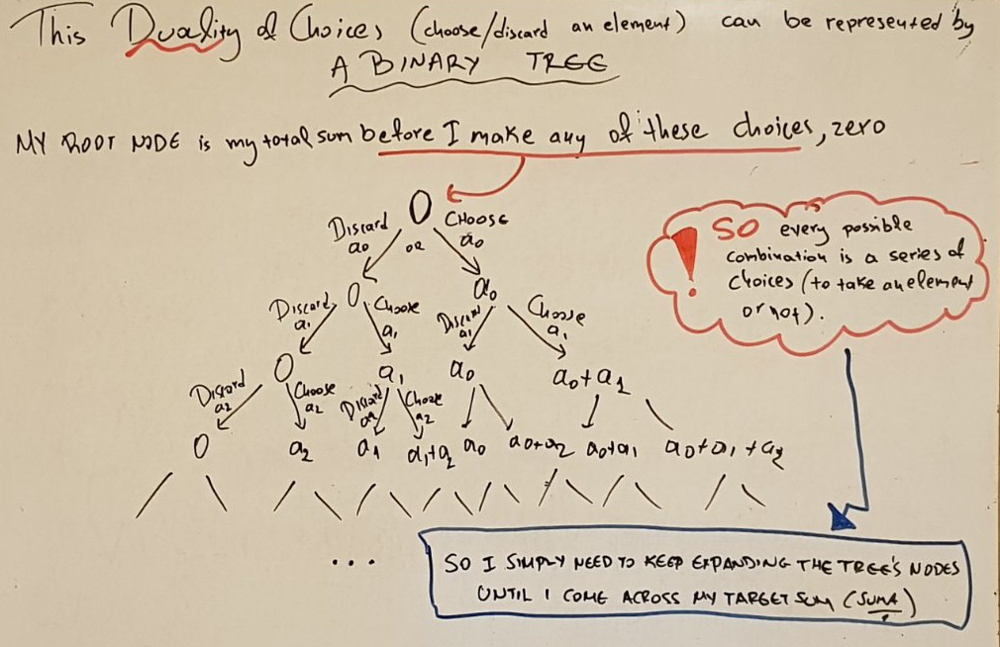
Let's demonstrate our solution with an example: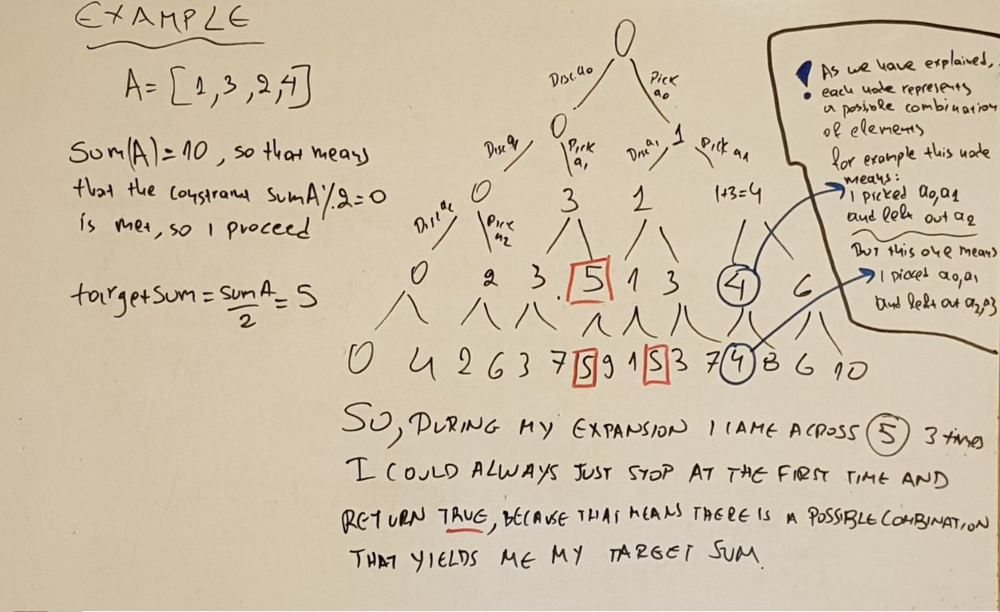
//clear backtracking, TLE
var canPartition = (candidates) => {
//sumA
let target=candidates.reduce((acc, curr) => acc + curr)
if (target%2) return false; //As we said our sum has to be dividible by two
target/=2
const backtracking = (currSum, index) => {
//if our Sum is bigger than my target there's no reason to continue expanding
if (currSum > target || index>=candidates.length)return false
// when I reach my target, return true
if (currSum === target)return true
return backtracking(currSum + candidates[index],index+1)||backtracking(currSum,index+1)
}
return backtracking(0,0)
}
//get's TLE'd on
//[1,1,...,1,1,100]
As you can see, this solution doesnt pass a certain case, we can easily remedy that by modifying our method a bit
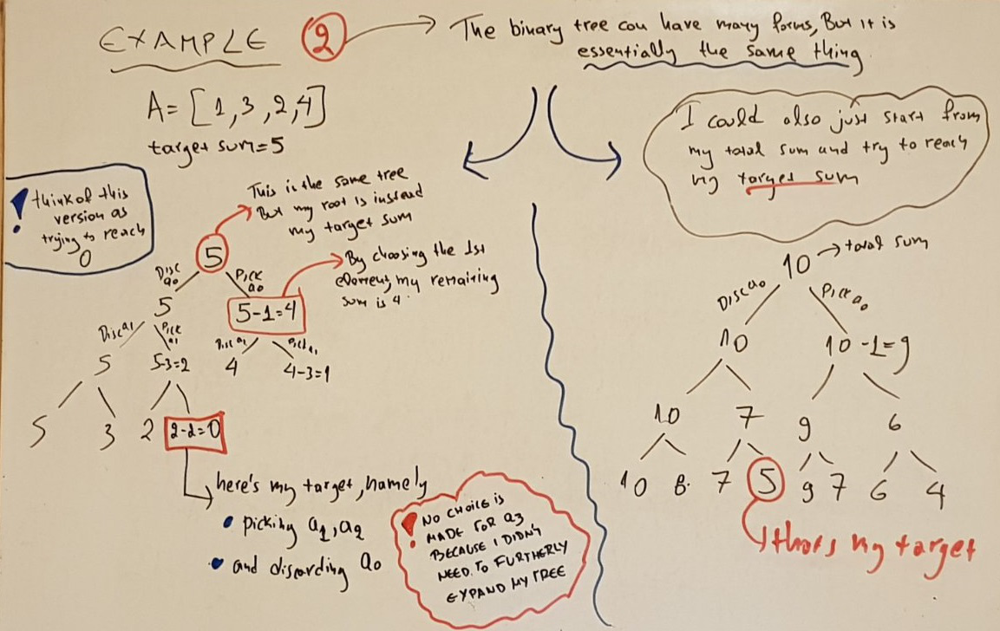
So If I start from my target and follow the first approach, I see that I pass all my cases:
var canPartition=candidates=>{
candidates.sort((a, b) => b- a); //key for TLE :Essentially means: If you fail,do it fast
let target=candidates.reduce((acc, curr) => acc + curr)
if (target%2) return false;
target/=2
const backtracking = (remaining, index) => {
if (remaining <candidates[index] || index>=candidates.length)return false
if (remaining === candidates[index])return true
return backtracking(remaining-candidates[index],index+1)||backtracking(remaining,index+1)
}
return backtracking(target,0)
}
KNAPSACK SOLUTION
Here follows some theoretical background for the knapsack problem, It is key to understand this in order to fully grasp the solutions that follow.
So, essentially, my task is to find the maximum value combination, given a capacity constraint.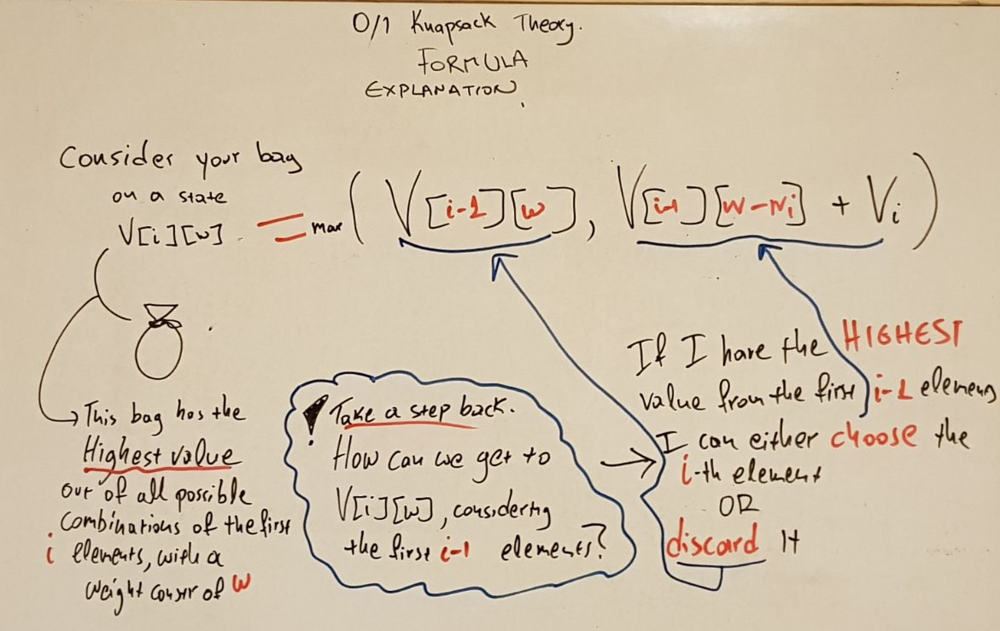
Let's dive into the formula
And here's a quick example for demonstration purposes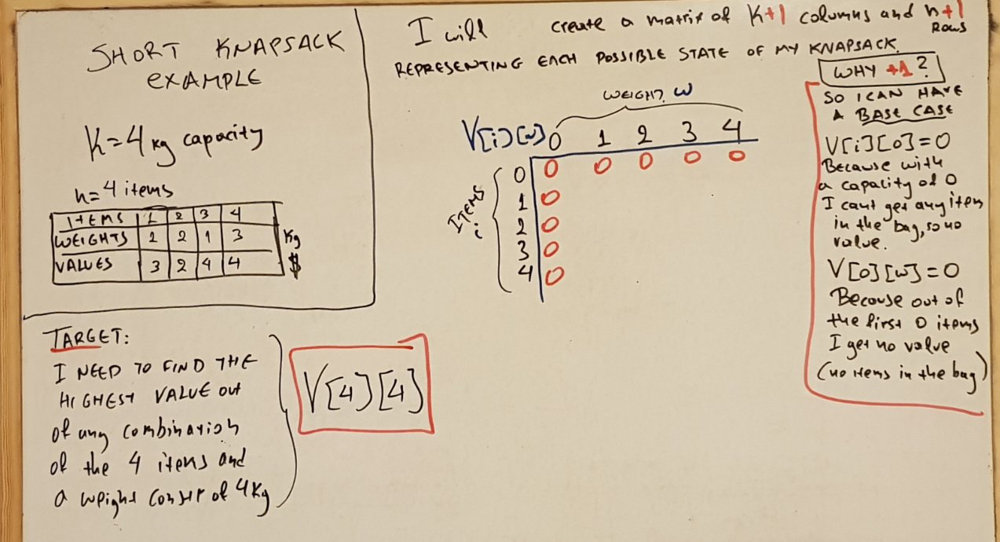
And here's the matrix completed
Back to my problem
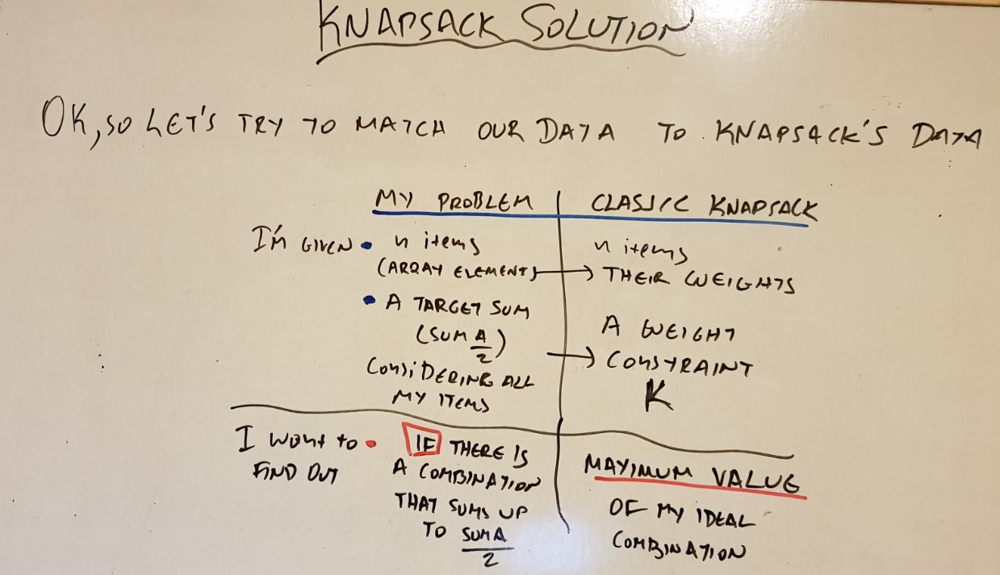
As you can see, my outputs are not identical. Here's how that affects my formula.
var canPartition = function(A) {
//calculate the sum of my Array
var sumA = A.reduce((acc, curr) => acc + curr);
if (sumA % 2) return false;
//create Rows
// i want a row for each of my candidate elements+ one for my
// 0th element( no element ) which I know for a fact can add up to 0 if selected
var B = new Array(A.length + 1).fill(null);
// create Columns
// My final total sum ranges from 0 to sumA, which are totally sumA+1 candidate weights(sums)
B = B.map(d => Array((sumA/2)+1).fill(false));
// now that the matrix is created I have to use my base case which is:
// If there is a way for me to get sum=0, with 0 elements
B[0][0] = true; // of course there is
//here i=0 cos everything other column (sum) of this row cannot be created with 0 elements
for (let i = 1; i <= A.length; i++) {
for (let j = 0; j <= sumA / 2 ; j++) {
//I know that i-1>=0 so i dont need an extra check for that
if (j - A[i - 1] >= 0){
B[i][j] = B[i - 1][j - A[i - 1]]||B[i - 1][j];
}
else{
B[i][j] = B[i - 1][j];
}
}
}
return B[A.length][sumA/2];
};
KNAPSACK OPTIMIZATIONS
There's room for improvement on my last solution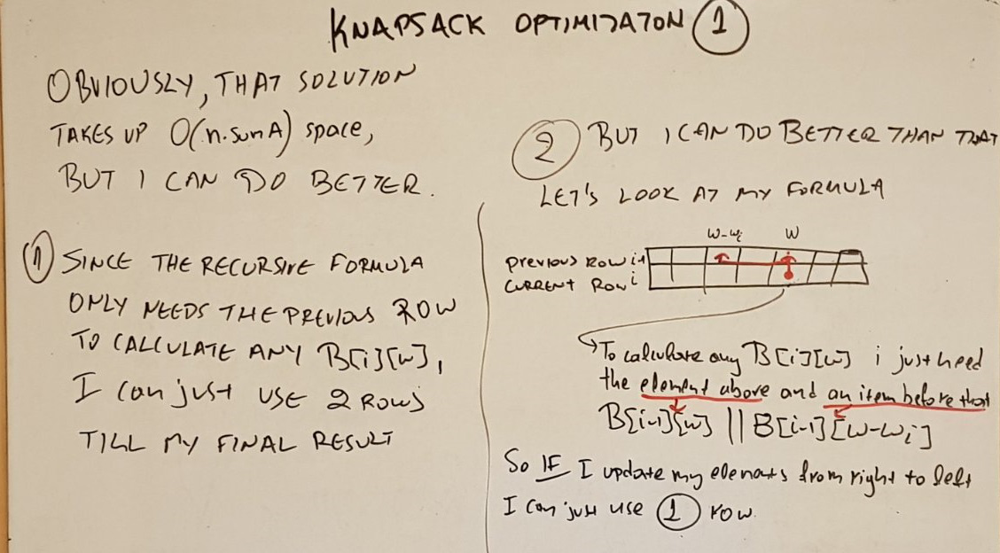
2ROW APPROACH
var canPartition = function(A) {
var sumA = A.reduce((acc, curr) => acc + curr);
if (sumA % 2) return false;
var previousRow = new Array((sumA/2)+1).fill(false);
var currentRow= new Array((sumA/2)+1).fill(false);
previousRow[0] = true; // base case
for (let i = 1; i <= A.length; i++) {
for (let j = 0; j <= sumA / 2 ; j++) {
if (j - A[i - 1] >= 0){
currentRow[j] = previousRow[j - A[i - 1]]||previousRow[j];
}
else{
currentRow[j] = previousRow[j];
}
}
previousRow=currentRow.slice(0) // make previous=current
}
return currentRow[sumA/2];
};
1 ROW APPROACH
var canPartition = function(A) {
var sumA = A.reduce((acc, curr) => acc + curr);
if (sumA % 2) return false;
var row = new Array((sumA/2)+1).fill(false);
row[0] = true; // base case
for (let i = 1; i <= A.length; i++) {
for (let j = sumA / 2; j >= 0; j--) { //start from right to left
if (j - A[i - 1] >= 0){
row[j] = row[j - A[i - 1]]||row[j];
}
}
}
return row[sumA/2];
};
FORWARD DYNAMIC PROGRAMMING STYLE
Essentially the two row approach, but a state [i][j] contributes to [i+1][j+A[i]] instead.
var canPartition = function(A) {
let totalSum=A.reduce((a,c)=>a+c),n=A.length
if(totalSum&1)
return false
let target=totalSum/2,
dp=[...Array(target+1)].map(d=>0),
dp2=[...Array(target+1)].map(d=>0)
dp[0]=1,dp[1]=1
for(let i=0;i<n;i++,dp=[...dp2])
for(let j=0;j<=target;j++)
if(j+A[i]<=target)
dp2[j+A[i]]|=dp[j]
return dp[target]
};
BIT SOLUTION
Here follows the final and more elegant approach using bitwise operations
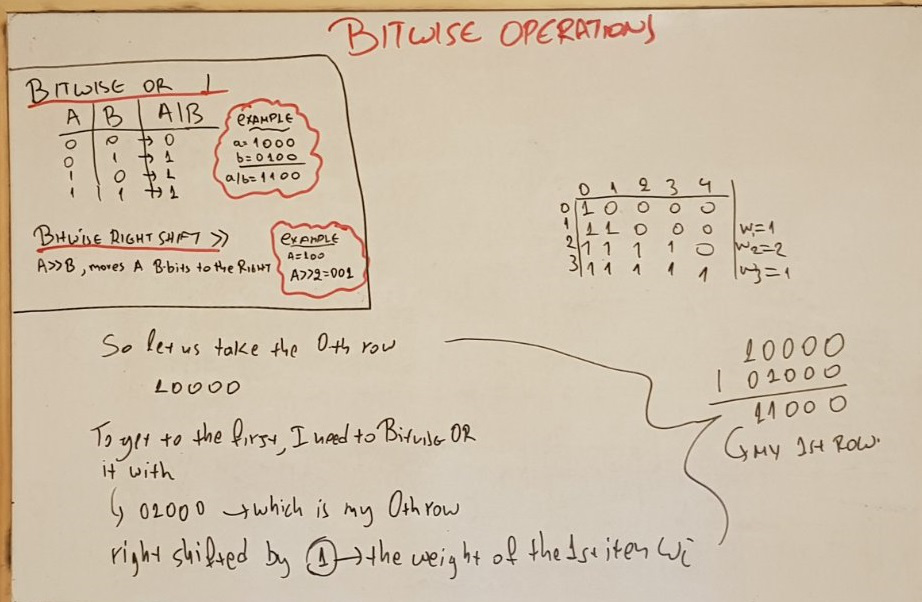
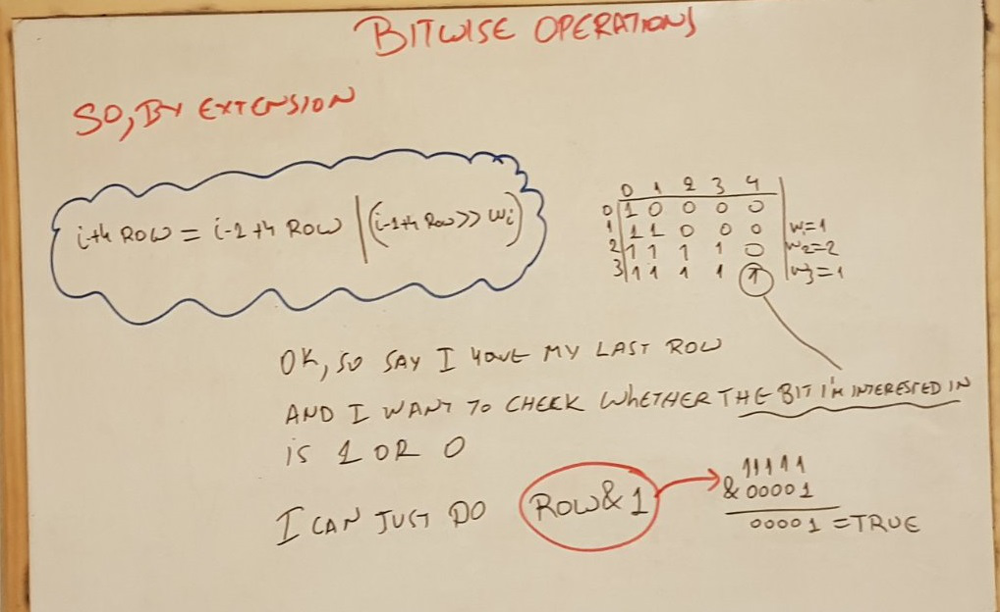
var canPartition = function(A) {
var sumA = A.reduce((acc, curr) => acc + curr)
/* to start with, i want the number with 1 as its first element so i can mimic the previous[0]=1 state, and length of bits= the length of bits of my desired sum (sumA/2)*/
if (sumA % 2)
return false;
let row = 1n << BigInt(sumA / 2 );
for (const weight of A)
row = row | (row >> BigInt(weight));
// check the the column corresponding to my target by bitwise ANDing it with just 1
// so if the first bit is 1, it will return true, otherwise false
return row&1n;
};
If you got this far, thank you for your attention. I hope I cleared up this problem. Sorry for my sloppy handwriting. Cheers.
January 4, 2020 8:13 AM
I commend you for the hard work put on explaining this problem. Very helpful. Thank you!
April 8, 2020 11:53 AM
best editorial ever!
August 6, 2020 4:46 AM
you should definitely try writing editorials for problems on leetcode 😉
March 6, 2020 5:10 PM
wow my dude, thank you
June 6, 2020 12:10 PM
OMG!!! This is heaven. Leant a lot from you mate! Hats off to your great work and thanks :)
July 11, 2020 4:47 AM
That's so much of hard work done for helping the rest of us. Thank you!
Last Edit: April 23, 2021 7:10 AM
Explained thoroughly.
Out of context:
Congratulations on maintaining the leetcode streak for 1 year straight. (I don't know how many years, since we can only see 1 year streak on leetcode. )
Sheer will!!
May 6, 2020 5:56 AM
Appreciates the amount of work you put in man <3
March 12, 2020 11:16 AM
Hi... regarding the fail fast solution, while it does pass the OJ test cases, it gives wrong result for [6,4,4,3,1]
Even if sum < arr[i], the smaller elements to the right might make the required sum. returning false give wrong answer.
Correcting this mistake again gives TLE on the previous test case.
December 18, 2021 4:50 AM
Backtracking with recursion fails for [14,9,8,4,3,2]
