June 21, 2022
Here is the article.
C# | Quick learner | Union find | DFS | 7 solutions | Top players -> improvements
June 13, 2022
It is hard to be a master of union find and DFS algorithm. I like to share my quick learning of C# solution after I chose to study various player solutions in weekly contest 112.
Also, I studied solutions written by various players, in weekly contest 112, ranking No. 5, 8, 12, 13, 16, 40, 58, 117, 176. The goal of my study is to read a lot of solutions, and learn to write a good one and enjoy the study. I did study those player code in 2019, and after three years, I like to share my C# solution as well.
I think that it is a good idea to put together 7 solutions in one discuss post, so that I can enjoy reading various ideas one time in C# programming language. After I read those ideas to write DFS or union find algorithms, I can expedite my thought process and write a short version in less than 30 minutes time.
Lee215 | Analysis | My understanding
I chose to study Lee215's analysis, and learn how to analyze the problem first.
Problem:
we can remove a stone if and only if,
there is another stone in the same column OR row.
We try to remove as many as stones as possible.
One sentence to solve:
Connected stones can be reduced to 1 stone,
the maximum stones can be removed = stones number - islands number.
so just count the number of "islands".
- Connected stones
Two stones are connected if they are in the same row or same col.
Connected stones will build a connected graph.
It's obvious that in one connected graph,
we can't remove all stones.
We have to have one stone left.
An intuition is that, in the best strategy, we can remove until 1 stone.
I guess you may reach this step when solving the problem.
But the important question is, how?
Lee215 | Union find algorithm | My understanding
I chose to study Lee215 analysis first.
- Union-Find
I use union find to solve this problem.
As I mentioned, the elements are not the points, but the indexes.
for each point, union two indexes.
return points number - union number
Copy a template of union-find,
write 2 lines above,
you can solve this problem in several minutes.
Complexity
union and find functions have worst case O(N), amortize O(1)
The whole union-find solution with path compression,
has O(N) Time, O(N) Space
Case study | Example 1 | All are connected
Input: stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
Output: 5
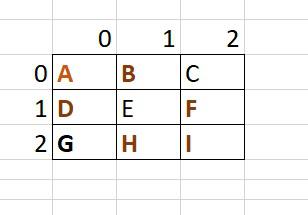
Given stones in the array [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]], and I mark the matrix 3 x 3 using A, B, C, D, E, F, G, those six elements are marked as A, B, D, F, H, I. A and B are connected in the same row, A and D are connected in the same column, D and F are connected in the same row, F and I are connected in the same column, H and I are connected in the same row, so A, B, D, F, H and I are all connected in one disjoint set. D, B, F, H, I can be removed, and only one node needs to stay as parent node in one disjoint set.
Union find algorithm - 15 minutes warmup
I always like to refresh my favorite lecture notes about union find algorithm lecture note.
https://algs4.cs.princeton.edu/15uf/
Every time I like to learn something new from the lecture notes. This time I like to quickly review weighted quick-union idea. It is fun to review algorithm in detail before I read C# implemented solutions.
Here are 7 various ideas to write DFS/ Union find algorithms. Read one or two if you have time. Also I like to review those top player's code and give some advice how to make improvements.
- DFS algorithm - Build an undirected graph, and then search using DFS - mark visited to avoid deadloop
- DFS algorithm - Similar to Item 2 DFS algorithm. Two players chose DFS, almost same. Solution 1 is to define undirected graph using List[1123], solution 2 is to define the graph using bool[1005][1005]. Only concern is sparse arrray, it is more space efficient to use List[1123], but List<IList> is best choice.
- Union find algorithm - with Rank option, I like to learn how to define Rank, first design concern is when to increment one, second one is to assign high rank to be parent node when two disjoint sets union together. In general, to write a working union find algorithm, there are at least three things to work on: path compression, quick union and also which one to be a root based on rank or size or other things.
- Union find algorithm - Only getRoot API with path compression
- Union find algorithm - getFather API with path compression
- Union find algorithm - union API, getParent API, quick-union and path compression
- Union algorithm - find API, union API, Size of disjoint set
It is one place to review all features of union find - how to define quick union, rank, size, and also path compression. I find that this is best and quick way to get familiar with union find algorithm and easy to review for a code assessment or learn an advanced graph algorithm.
I think that it is important to review DFS solution first, since it takes less time to write and also easy to follow.
Solution 1: DFS
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_remove_stones_rank_16
{
class Program
{
/// <summary>
/// Leetcode 947 remove stones
/// </summary>
/// <param name="args"></param>
static void Main(string[] args)
{
RunTestcase2();
}
public static void RunTestcase1()
{
var stones = new int[6][]{
new int[]{0,0},
new int[]{0,1},
new int[]{1,0},
new int[]{1,2},
new int[]{2,1},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
public static void RunTestcase2()
{
var stones = new int[5][]{
new int[]{0,0},
new int[]{0,2},
new int[]{1,1},
new int[]{2,0},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
public static List<int>[] graph = new List<int>[1123];
public static int[] Visited = new int[1123];
/// <summary>
/// study code
/// https://leetcode.com/contest/weekly-contest-112/ranking/
/// Ranking No. 16 sohelH
/// Two tips to construct a undirected graph
/// 1. brute force all possible edges
/// 2. check if two nodes are in the same row or same column. If it is same row or column,
/// then the two nodes are connected.
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
int length = stones.Length;
for (int i = 0; i < length; i++)
{
graph[i] = new List<int>();
Visited[i] = 0;
}
for (int i = 0; i < length; i++)
{
for (int j = i + 1; j < length; j++)
{
int r1 = stones[i][0];
int c1 = stones[i][1];
int r2 = stones[j][0];
int c2 = stones[j][1];
if (r1 == r2 || c1 == c2)
{
graph[i].Add(j);
graph[j].Add(i);
}
}
}
int components = 0;
for (int i = 0; i < length; i++)
{
if (Visited[i] == 0)
{
dfs(i);
components++;
}
}
return length - components;
}
private static void dfs(int u)
{
if (Visited[u] == 1)
{
return;
}
Visited[u] = 1;
for (int i = 0; i < graph[u].Count; i++)
{
dfs(graph[u][i]);
}
}
}
}
Here is another DFS solution. I like to read C# code and think about how to improve the code.
Solution 2: DFS | Second solution of DFS
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_remove_stones___DFS
{
class Program
{
/// <summary>
/// Leetcode 947 remove stones
/// </summary>
/// <param name="args"></param>
static void Main(string[] args)
{
RunTestcase2();
}
public static void RunTestcase1()
{
var stones = new int[6][]{
new int[]{0,0},
new int[]{0,1},
new int[]{1,0},
new int[]{1,2},
new int[]{2,1},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
public static void RunTestcase2()
{
var stones = new int[5][]{
new int[]{0,0},
new int[]{0,2},
new int[]{1,1},
new int[]{2,0},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
public static int Rows;
public static bool[][] graph = new bool[1005][];
public static bool[] visited = new bool[1005];
/// <summary>
/// study code
/// https://leetcode.com/contest/weekly-contest-112/ranking/
/// Ranking No. 5 joon_young
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
Rows = stones.Length;
for (int row = 0; row < 1005; row++)
{
graph[row] = new bool[1005];
}
// reset to false
for (int row = 0; row < 1005; row++)
{
visited[row] = false;
}
for (int row = 0; row < Rows; row++)
{
for (int j = row + 1; j < Rows; j++)
{
if (stones[row][0] == stones[j][0] ||
stones[row][1] == stones[j][1])
{
graph[row][j] = true;
graph[j][row] = true;
}
}
}
int result = 0;
for (int row = 0; row < Rows; row++)
{
if(visited[row])
{
continue;
}
result++;
dfs(row);
}
return Rows - result;
}
private static void dfs(int id)
{
if (visited[id])
return;
visited[id] = true;
for (int row = 0; row < Rows; row++)
{
if (graph[id][row])
{
dfs(row);
}
}
}
}
}
Solution 3: Union find - Rank
The following C# code passes online judge.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_remove_stones___union_join
{
class Program
{
static void Main(string[] args)
{
var stones = new int[6][]{
new int[]{0,0},
new int[]{0,1},
new int[]{1,0},
new int[]{1,2},
new int[]{2,1},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
public static int[] Parent;
public static int[] Size;
public static int[] Rank;
public static int Total;
/// <summary>
/// https://leetcode.com/contest/weekly-contest-112/ranking
/// rank No. 13 yangmei555
///
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
var length = stones.Length;
Parent = new int[length];
Size = new int[length];
Rank = new int[length];
for (int i = 0; i < length; i++)
{
Parent[i] = i;
Size[i] = 1;
}
Total = length;
for (int i = 0; i < length; i++)
{
for (int j = i + 1; j < length; j++)
{
if (stones[i][0] == stones[j][0] ||
stones[i][1] == stones[j][1])
{
union(i, j);
}
}
}
return length - Total;
}
/// <summary>
/// code review:
/// union and rank is simplified, and this version of code is easy to follow
/// Rule 1: Parent node has higher rank compared to its child node
/// union is to connect two root nodes of tree.
/// </summary>
/// <param name="i"></param>
/// <param name="j"></param>
private static void union(int i, int j)
{
int id1 = find(i);
int id2 = find(j);
if (id1 != id2)
{
Total--;
if (Rank[id1] <= Rank[id2])
{
Parent[id1] = id2;
if (Rank[id1] == Rank[id2])
{
Rank[id2]++;
}
}
else
{
Parent[id2] = id1;
}
}
}
/// <summary>
/// code review:
/// find is to search tree structure and find the root of tree the node stays
/// </summary>
/// <param name="id"></param>
/// <returns></returns>
private static int find(int id)
{
if (id != Parent[id])
{
Parent[id] = find(Parent[id]);
}
return Parent[id];
}
}
}
4th solution: Union find algorithm
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_ranking_117
{
class Program
{
public static void RunTestcase2()
{
var stones = new int[7][]{
new int[]{3, 3},
new int[]{4, 4},
new int[]{1, 4},
new int[]{1, 5},
new int[]{2, 3},
new int[]{4, 3},
new int[]{2, 4}
};
var number = RemoveStones(stones);
}
static void Main(string[] args)
{
RunTestcase2();
}
/// <summary>
/// https://leetcode.com/contest/weekly-contest-112/ranking/5/
/// rank 117
/// yajingleo
///
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
var length = stones.Length;
var root = new int[length];
for (int i = 0; i < length; i++)
{
root[i] = i;
}
for (int i = 0; i < length; i++)
{
for (int j = 0; j < length; j++)
{
if (stones[i][0] == stones[j][0] || stones[i][1] == stones[j][1])
{
var root1 = getRoot(root, i);
var root2 = getRoot(root, j);
// given constraint on the root, smaller index will be the root.
root[root2] = root1;
}
}
}
int result = length;
for(int i = 0; i < length; i++)
{
if(root[i] == i)
{
result--;
}
}
return result;
}
/// <summary>
/// code review April 4, 2019
/// It is better to use while loop instead of recursive function
/// </summary>
/// <param name="root"></param>
/// <param name="i"></param>
/// <returns></returns>
private static int getRoot(int[] root, int i)
{
while (root[i] != i)
{
i = root[i];
}
return i;
}
}
}
Solution 5: Union find algorithm
It is interesting to read the code related to how to determine which one should be the parent when two nodes join the same disjoint set. The node with higher index is selected to be the root of disjoint set.
for (int i = 0; i < rows; i++)
{
for (int j = i + 1; j < rows; j++)
{
if (stones[i][0] == stones[j][0] || stones[i][1] == stones[j][1])
{
int fi = getFather(i);
int fj = getFather(j);
father[fi] = fj;
}
}
}
Pay attention to the above double for loop, second loop variable j > i, and then j's parent will be i's parent's parent. Interesting? How to avoid writing code related to rank, it is quick and easy way to make it consistent this way.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_remove_stones
{
class Program
{
static void Main(string[] args)
{
var stones = new int[6][]{
new int[]{0,0},
new int[]{0,1},
new int[]{1,0},
new int[]{1,2},
new int[]{2,1},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
private static List<int> father;
/// <summary>
///
/// </summary>
/// <param name="i"></param>
/// <returns></returns>
private static int getFather(int search)
{
if (search == father[search])
{
return search;
}
int root = getFather(father[search]);
father[search] = root;
return root;
}
/// <summary>
/// Leetcode 947
/// https://leetcode.com/contest/weekly-contest-112/ranking/
/// ranking 8
/// Windsfantasy6
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
var rows = stones.Length;
father = new List<int>();
for (int i = 0; i < rows; i++)
{
father.Add(i);
}
for (int i = 0; i < rows; i++)
{
for (int j = i + 1; j < rows; j++)
{
if (stones[i][0] == stones[j][0] || stones[i][1] == stones[j][1])
{
int fi = getFather(i);
int fj = getFather(j);
father[fi] = fj;
}
}
}
// Disjoint set count upper limit -> total number of rows or columns
int result = 0;
for (int i = 0; i < rows; i++)
{
int fi = getFather(i);
if (i == fi)
{
result++;
}
}
return rows - result;
}
}
}
Solution 6: Union find algorithm
I learned the lesson, and getParent API should be called instead of calling parent[i].
It is better to go over lecture notes to review union find algorithm first.
https://algs4.cs.princeton.edu/15uf/
https://algs4.cs.princeton.edu/15uf/QuickUnionPathCompressionUF.java.html
It is important to understand path compression, the binary tree should be flated and it is more efficient to do that. Also I need to learn again quick-union and path compression, getParent API has path-compression, and union API is a quick-union time complexity O(1) operation.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_remove_stones_Rank_176
{
class Program
{
static void Main(string[] args)
{
RunTestcase1();
}
public static void RunTestcase1()
{
var stones = new int[7][]{
new int[]{3, 2},
new int[]{0, 0},
new int[]{3, 3},
new int[]{2, 1},
new int[]{2, 3},
new int[]{2, 2},
new int[]{0, 2}
};
var number = RemoveStones(stones);
}
// [[3,3],[4,4],[1,4],[1,5],[2,3],[4,3],[2,4]]
public static void RunTestcase2()
{
var stones = new int[7][]{
new int[]{3, 3},
new int[]{4, 4},
new int[]{1, 4},
new int[]{1, 5},
new int[]{2, 3},
new int[]{4, 3},
new int[]{2, 4}
};
var number = RemoveStones(stones);
}
/// <summary>
/// study code weekly contest 112
/// Rank 176
/// https://leetcode.com/contest/weekly-contest-112/ranking/8/
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
var length = stones.Length;
for (int i = 0; i < length; i++)
{
Parent[i] = i;
}
for (int i = 0; i < length; i++)
{
for (int j = i + 1; j < length; j++)
{
if (stones[i][0] == stones[j][0] || stones[i][1] == stones[j][1])
{
if (Parent[i] != Parent[j])
{
union(i, j);
}
}
}
}
int number = 0;
for (int i = 0; i < length; i++)
{
if(i == Parent[i])
{
number++;
}
}
return length - number;
}
public static int[] Parent = new int[1005];
public static int[] Rank = new int[1005];
/// <summary>
/// path compression
/// https://algs4.cs.princeton.edu/15uf/QuickUnionPathCompressionUF.java.html
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
private static int getParent_Obsolete(int x)
{
while (Parent[x] != x)
{
x = Parent[x];
}
return x;
}
/// <summary>
/// study code from
/// https://algs4.cs.princeton.edu/15uf/QuickUnionPathCompressionUF.java.html
/// </summary>
/// <param name="p"></param>
/// <returns></returns>
public static int getParent(int p)
{
int root = p;
while (root != Parent[root])
{
root = Parent[root];
}
while (p != root)
{
int newp = Parent[p];
Parent[p] = root;
p = newp;
}
return root;
}
/// <summary>
/// this function has a bug
/// var root1 = Parent[id1] -- should be -> var root1 = getParent(id1)
/// In other words, I need to separate intermediate node from root node of tree.
/// </summary>
/// <param name="id1"></param>
/// <param name="id2"></param>
private static void union_Buggy(int id1, int id2)
{
var root1 = Parent[id1];
var root2 = Parent[id2];
Parent[root2] = root1;
}
private static void union(int id1, int id2)
{
var root1 = getParent(id1);
var root2 = getParent(id2);
Parent[root2] = root1;
}
}
}
Solution 7: Union find algorithm
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _947_remove_stones___union_join
{
class Program
{
static void Main(string[] args)
{
var stones = new int[6][]{
new int[]{0,0},
new int[]{0,1},
new int[]{1,0},
new int[]{1,2},
new int[]{2,1},
new int[]{2,2}
};
var result = RemoveStones(stones);
}
public static int[] Size = new int[1005];
public static int[] Parent = new int[1005];
/// <summary>
/// https://leetcode.com/contest/weekly-contest-112/ranking
/// rank No. 40 biltharesatyendra
///
/// </summary>
/// <param name="stones"></param>
/// <returns></returns>
public static int RemoveStones(int[][] stones)
{
var length = stones.Length;
for (int i = 0; i < length; i++)
{
Parent[i] = i;
Size[i] = 1;
}
for (int i = 0; i < length; i++)
{
for (int j = i + 1; j < length; j++)
{
if (stones[i][0] == stones[j][0] ||
stones[i][1] == stones[j][1])
{
union(i, j);
}
}
}
// count of disjoint sets
int answer = 0;
for (int i = 0; i < length; i++)
{
if (find(i) == i)
{
answer += Size[i] - 1;
}
}
return answer;
}
/// <summary>
/// code review:
/// union and rank is simplified, and this version of code is easy to follow
/// Rule 1: Parent node has higher rank compared to its child node
/// union is to connect two root nodes of tree, not input arguments id1 and id2.
/// </summary>
/// <param name="i"></param>
/// <param name="j"></param>
private static void union(int id1, int id2)
{
id1 = find(id1); // To avoid the bug to confuse id1 and find(id1), change id1's value
id2 = find(id2);
if (id1 == id2)
{
return;
}
if (Size[id1] < Size[id2])
{
swap(ref id1, ref id2);
};
Parent[id2] = id1;
Size[id1] += Size[id2];
}
public static void swap(ref int x, ref int y)
{
var tmp = x;
x = y;
y = tmp;
}
/// <summary>
/// code review:
/// find is to search tree structure and find the root of tree the node stays
/// </summary>
/// <param name="id"></param>
/// <returns></returns>
private static int find(int id)
{
if (id != Parent[id])
{
Parent[id] = find(Parent[id]);
}
return Parent[id];
}
}
}
No comments:
Post a Comment