Leetcode discuss: 84. Largest Rectangle in Histogram

July 19, 2022

Here is the link. 

C# | Quick learner | Optimal time complexity solution provided

Dec. 3, 2020
I work on five solutions and I like to share the solution using stack with optimal time complexity O(N^2). Also, I add brute force solution as solution 2, which may not be helpful for any interview preparation, O(N^3).

All solutions in series:

1. Brute force
2. Better brute force
3. Divide and conquer
4. Better divide and conquer
5. Using stack

Solution 1: Using stack | Time complexity: O(N)

Example | Case study | Ask good questions
It is a hard level algorithm. Every one should think about using stack to reach optimal time complexity O(N). But how to maintain the stack and keep ascending stack to meet calculation need. I like to contribute some good thoughts so that you and I both learn something.

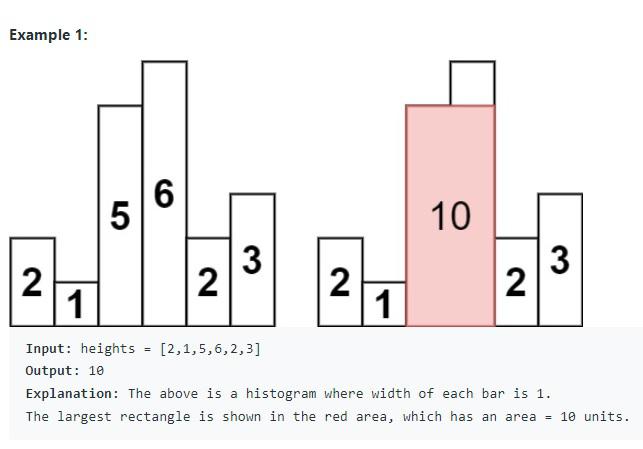
How to calculate the largest histogram area - 10, what is in stack when iteration to index = 4, value 2, I believe that maximum area will calculate including 6 - as one standalone, and then two - 5 and 6, and then 6 should be popped from stack, 6 should be popped from 5, since 5 and 6 will no longer be needed in any calculation for possible bigger area any more.

One thing to argue is that the stack should always keep the minimum value in the stack before it reaches the last one in the stack. That one is possible candidate for largest histogram area, using minimum value multiplys the length of the array.

Calculation when index = 4, value 2

1. Pop 6 since 6 > 2 - calculate area 6 -> 6, compare to maximum area so far
2. Pop 5 since 5 > 2 - calculate area from 5, 6 -> 10, compare to maximum area so far
3. Compare 1 vs 2, leave 1 in stack, no calculation, push 2 into the stack, {1, 2}. 

Think about the above steps, see if anything is wrong or missing anything for possible largest histogram area.

Go back and forth to warm up the algorithm design using the above histogram, ask more questions. Using debugger, and then make sure that the argument is true or false.

Requirement analysis:
I reviewed a few videos on youtube.com related to this algorithm. I do think that the missing part in those video is about how to analyze starting from brute force, and come out requirement for optimal solution:

1. Need to find minimum value in the array, for width of span of whole array.
2. Need to find maximum value in the array, for only one number area;
3. Need to argue that ascending order numbers, we can skip multiple areas for one number, two numbers, three numbers etc. to one of them, as long as we count the numbers from highest to smaller ones in consecutive orders. (This is interesting math problem, we can prove that it is true.)
4. Next extract the design of data structure of ascending stack.
5. We need to make sure that for all width from 1 to n, n is the length of the array, we need to select at least one of them, maximum one should be included.
6. More on step 5, relax on this requirement, we can find multiple time as long as we maintain the ascending stack, and pop up those numbers bigger than current number.

public class Solution {
    public int LargestRectangleArea(int[] height) {
            var stack = new Stack<int>();

            var index = 0;
            var largestArea = 0;

            int length = height.Length; // 6

            while (index < length) // true; index = 1; index = 2;
            { 
                //     stack empty            going upward
                if (stack.Count == 0 || height[stack.Peek()] < height[index]) // index = 1, false;
                {
                    stack.Push(index++); // 0, index = 1;
                }
                else
                {
                    // going downward and then pop stack, calculate rectangle.
                    popStackAndCalculate(ref largestArea, stack, height, index);
                }
            }

            while (stack.Count > 0)
            {
                popStackAndCalculate(ref largestArea, stack, height, length);
            }

            return largestArea;
        }

        /// <summary>
        /// downward and then pop stack to calculate the rectangle
        /// </summary>
        /// <param name="largestArea"></param>
        /// <param name="stack"></param>
        /// <param name="height"></param>
        private static void popStackAndCalculate(ref int largestArea, Stack<int> stack, int[] height, int rightIndex)
        {
            int length = height.Length; // 6

            int lastHeight = height[stack.Pop()]; // 2
            int width = stack.Count == 0 ? rightIndex : rightIndex - stack.Peek() - 1; // 1

            largestArea = Math.Max(largestArea, lastHeight * width); // 2 * 1
        }
}

Solution 2: Brute force solution | Naive approach
I like to quickly share the brute force solution. This is a good exercise to review basics of for loop and make sure that calculation is correct first.

Five series - C# - Brute force - TLE - Time O(N^3)

Consider every possible pair of bars, and find the area of the rectangle formed between them using the height of the shortest bar lying between them as the height and the spacing between them as the width of the rectangle. We can thus, find the required rectangle with the maximum area.

public class Solution {
    /// <summary>
        /// brute force solution
        /// Time complexity: O(N^3)
        /// start and end position - all possible pairs - O(N^2)
        /// Find minimum height in given range - O(N)
        /// Total time complexity is O(N^3). 
        /// </summary>
        /// <param name="heights"></param>
        /// <returns></returns>
        public int LargestRectangleArea(int[] heights)
        {
            var length = heights.Length; 
            int maxarea = 0;

            for (int start = 0; start < length; start++)
            {
                for (int end = start; end < length; end++)
                {
                    var minHeight = Int32.MaxValue;

                    for (int k = start; k <= end; k++)
                    {
                        minHeight = Math.Min(minHeight, heights[k]);
                    }

                    maxarea = Math.Max(maxarea, minHeight * (end - start + 1));
                }
            }

            return maxarea;
        }
}