May 19, 2022
Here is the link.
This is very useful technique, which uses both idea of bitmasks and dymamic programming. What is bitmask? It is specific way to represent data, where 1 means that element is taken and 0 that it is not taken. For example if nums = [1,2,8,9,10], than bitmask 01011 represents set {2, 9, 10}. Of course we can use sets as well, but bitmask make it very fast and efficient.
There is a bunch of leetcode problems (usually they are hard, but sometimes medium as well). Imagine the following problem as examples: given 2n points on the plane we need to construct n segments, using all 2n points, such that sum of length of these segments is minimal. The idea is to keep bitmask of already used nodes: for example 00011101 mask means that we use nodes number 0, 2, 3, 4. Now the question is how to go from one mask to another: we can do it in 6 ways here: 11011101, 10111101, 10011111, 01111101, 01011111, 00111111. In general we will have 2^n masks and O(n^2) ways to go from one mask to another. Now, when you get the idea of how it works let us consider several problems from leetcode, where this idea can be applied:
Problem 698: Partition to K Equal Sum Subsets
https://leetcode.com/problems/partition-to-k-equal-sum-subsets/
Denote by dp[mask] possibility to put numbers with mask mask into our subsets. In more detais: we return -1 if this partition is not possible and we return t >= 0, if it is possible, where t is reminder when we divide sum of all used numbers so far by basket: value, of how many we need to put in each group. Then to check if we can do it, we need to check the last number we put and check n possible options, where n is number of nums. Overall time complexity is (2^n * n) and space complexity is O(2^n).
class Solution:
def canPartitionKSubsets(self, nums, k):
N = len(nums)
nums.sort(reverse = True)
basket, rem = divmod(sum(nums), k)
if rem or nums[0] > basket: return False
dp = [-1] * (1<<N)
dp[0] = 0
for mask in range(1<<N):
for j in range(N):
neib = dp[mask ^ (1<<j)]
if mask & (1<<j) and neib >= 0 and neib + nums[j] <= basket:
dp[mask] = (neib + nums[j]) % basket
break
return dp[-1] == 0
Problem 473 Matchsticks to Square
https://leetcode.com/problems/matchsticks-to-square/
Special case of Problem 698 Partition to K Equal Sum Subsets, but here we need to partition into 4 equal sums (we say, put them into buckets). So actually we can reuse exactly the same code we did in Problem 698, but here I do it in different way, using @lru_cache(None), which is used for memoisation. Time complexity is O(2^n*n), space complexity is O(2^n).
class Solution:
def makesquare(self, nums):
N = len(nums)
basket, rem = divmod(sum(nums), 4)
if rem or nums[0] > basket: return False
@lru_cache(None)
def dfs(mask):
if mask == 0: return 0
for j in range(N):
if mask & 1<<j:
neib = dfs(mask ^ 1<<j)
if neib >= 0 and neib + nums[j] <= basket:
return (neib + nums[j]) % basket
return -1
return dfs((1<<N) - 1) == 0
526. Beautiful Arrangement
https://leetcode.com/problems/beautiful-arrangement/
Let us use dynamic programming with bitmasks. The idea is to use function dfs(bm, pl), where:
bmis binary mask for visited numbers.plis current place we want to fill. Idea is to start from the end, and fill places in opposite direction, because for big numbers we potentially have less candidates. (if we start formpl = 0and go in increasing direction, then it is also will work fine, like120msvs60ms)
Now, let us discuss how dfs(bm, pl) will work:
- If we reached place
0and procces was not interrupted so far, it means that we find beautiful arrangement. - For each number
1, 2, ..., Nwe try to put this number on placepl: and we need to check two conditions: first, that this place is still empty, using bitmask and secondly that one of the two properties for beutiful arrangement holds. In this case we adddfs(bm^1<<i, pl - 1)to final answer. - Finally, we run
dfs(0, N): from the last place and with empty bit-mask.
Complexity: First of all, notice that we have 2^N possible options for bm, N possible options for pl. But in all we have only 2^N states: pl is uniquely defined by number of nonzero bits in bm. Also we have N possible moves from one state to another, so time complexity is O(N*2^N). Space complexity is O(2^N).
class Solution:
def countArrangement(self, N):
@lru_cache(None)
def dfs(bm, pl):
if pl == 0: return 1
S = 0
for i in range(N):
if not bm&1<<i and ((i+1)%pl == 0 or pl%(i+1) == 0):
S += dfs(bm^1<<i, pl - 1)
return S
return dfs(0, N)
Problem 847 Shortest Path Visiting All Nodes
https://leetcode.com/problems/shortest-path-visiting-all-nodes/
Let us first find distances between all pairs of nodes, using either bfs or better Floyd-Warshall algorithm with O(n^3) complexity. (do not be afraid of this algorithm, in fact it is just usual dp, but it is not the point of interest here, we want to focus on dp on subsets.
Then our problem is equivalent to Traveling Salesman Problem (TSP): we need to find path with smallest weight, visiting all nodes. Here we have 2^n * n possible states, where state consists of two elements:
mask: binary mask with lengthnwith already visited nodes.last: last visited node.
Note, that it is wary similar to previous approach we used, but now we need to include last visited node in our state.
There will be O(n) possible transitions for each state: for example to the state (10011101, 7) we will have possible steps from (00011101, 0), (00011101, 2), (00011101, 3), (00011101, 4). Finally, time complexity is O(2^n*n^2) and space complexity is O(2^n*n).
class Solution:
def shortestPathLength(self, graph):
n = len(graph)
W = [[float("inf")] * n for _ in range(n)]
#for i in range(n): W[i][i] = 0
for i in range(n):
for j in graph[i]:
W[i][j] = 1
for i,j,k in product(range(n), repeat = 3):
W[i][j] = min(W[i][j], W[i][k] + W[k][j])
dp = [[float("inf")] * n for _ in range(1<<n)]
for i in range(n): dp[1<<i][i] = 0
for mask in range(1<<n):
n_z_bits = [j for j in range(n) if mask&(1<<j)]
for j, k in permutations(n_z_bits, 2):
cand = dp[mask ^ (1<<j)][k] + W[k][j]
dp[mask][j] = min(dp[mask][j], cand)
return min(dp[-1])
Problem 943 Find the Shortest Superstring
https://leetcode.com/problems/find-the-shortest-superstring/
This is actually Travelling salesman problem (TSP) problem: if we look at our strings as nodes, then we can evaluate distance between one string and another, for example for abcde and cdefghij distance is 5, because we need to use 5 more symbols fghij to continue first string to get the second. Note, that this is not symmetric, so our graph is oriented. Our state will be (bitmask, last) as in problem 847.
Complexity is O(n^2 * 2^n), because every state is bitmask + last visited node. In each dp[i][j] we will keep length of built string + built string itself.
class Solution:
def shortestSuperstring(self, A):
@lru_cache(None)
def connect(w1, w2):
return [w2[i:] for i in range(len(w1) + 1) if w1[-i:] == w2[:i] or not i][-1]
N = len(A)
dp = [[(float("inf"), "")] * N for _ in range(1<<N)]
for i in range(N): dp[1<<i][i] = (len(A[i]), A[i])
for mask in range(1<<N):
n_z_bits = [j for j in range(N) if mask & 1<<j]
for j, k in permutations(n_z_bits, 2):
cand = dp[mask ^ 1<<j][k][1] + connect(A[k], A[j])
dp[mask][j] = min(dp[mask][j], (len(cand), cand))
return min(dp[-1])[1]
Problem 1434 Number of Ways to Wear Different Hats to Each Other
https://leetcode.com/problems/number-of-ways-to-wear-different-hats-to-each-other/
Here our state is dp[mask][hat_id], where mask is bitmask for used people and hat_id is number of hats we processed so far. Number of states is O(2^n*m), where n is number of people and m is number of people. So, time complexity is O(2^n*n*m).
class Solution:
def numberWays(self, hats):
n, M, N_hats = len(hats), 10**9 + 7, 41
hats_persons = defaultdict(set)
for person_id, person in enumerate(hats):
hats_persons[person_id] = set(person)
dp = [[0] * N_hats for _ in range(1<<n)]
dp[0][0] = 1
for mask in range(0, 1<<n):
for hat_id in range(N_hats):
for person in range(n):
neib = mask ^ 1<<(person)
if neib != mask and hat_id in hats_persons[person]:
dp[mask][hat_id] += dp[neib][hat_id-1]
dp[mask][hat_id] = (dp[mask][hat_id] + dp[mask][hat_id-1]) % M
return int(dp[-1][-1] % M)
Problem 1494 Parallel Courses II
https://leetcode.com/problems/parallel-courses-ii/
Let us denote by dp[i][j] tuple with:
- minumum number of days we need to finish
- number of non-zero bits for binary mask of the last semester
- binary mask of the last semester
all courses denoted by binary mask i and such that the last course we take is j. For example for dp[13][3], i=13 is represented as 1101, and it means that we take courses number 0, 2, 3 and the last one we take is number 3. (instead of starting with 1, let us subtract 1 from all courses and start from 0).
Let us also introduce bm_dep[i]: this will be binary mask for all courses we need to take, before we can take course number i. For example bm_dep[3] = 6 = 110 means, that we need to take courses 1 and 2 before we can take course number 3.
Now, let us iterate over all i in range(1<<n). Let us evaluate n_z_bit, this will be an array with all places with non-zero bits. For example for i=13=1101, n_z_bit = [0,2,3].
What we need to do next, we:
- First check that we really can take new course number
j, usingbm_dep[j] & i == bm_dep[j]. - Now, we want to update
dp[i][j], usingdp[i^(1<<j)][t], for example if we want to find answer for(1,3,4,5)courses with3being the last course, it means that we need to look into(1,4,5)courses, where we add course3. - We check how many courses we already take in last semester, using
bits < k, and also make sure, that we can add new course to last semester. Now we have two candidates:(cand, bits + 1, mask + (1<<j))anddp[i][j]and we need to choose the best one. In other case, we need to take new semester: socandswill be equalt tocands + 1,bitswill be equal to1and binary mask for last semester is1<<j.
Complexity is O(n^2*2^n), because we iterate all bitmasks and then we iterate over all pairs of non-zero bit, and we heve O(n^2) of them. Memory is O(2^n * n).
I think it can be simplified to O(n*2^n)/O(2^n) complexity, but I am not sure yet.
class Solution:
def minNumberOfSemesters(self, n, dependencies, k):
dp = [[(100, 0, 0)] * n for _ in range(1<<n)]
bm_dep = [0]*(n)
for i,j in dependencies:
bm_dep[j-1]^=(1<<(i-1))
for i in range(n):
if bm_dep[i] == 0: dp[1<<i][i] = (1, 1, 1<<i)
for i in range(1<<n):
n_z_bits = [len(bin(i))-p-1 for p,c in enumerate(bin(i)) if c=="1"]
for t, j in permutations(n_z_bits, 2):
if bm_dep[j] & i == bm_dep[j]:
cand, bits, mask = dp[i^(1<<j)][t]
if bm_dep[j] & mask == 0 and bits < k:
dp[i][j] = min(dp[i][j], (cand, bits + 1, mask + (1<<j)))
else:
dp[i][j] = min(dp[i][j], (cand+1, 1, 1<<j))
return min([i for i, j, k in dp[-1]])
Problem 1655 Distribute Repeating Integers
https://leetcode.com/problems/distribute-repeating-integers/
Let us precalculate sums of all subsets first for speed. Let us define our state as dfs(i, mask), where i is index not of customer, but Counter(nums):
Imagine we have Counter(nums) = 10, 5 and quantities = 5,7,3, then we first try to distribute 10: on different bitmasks: 000, 001, 010, 011, 100, 101, 110, 111, here we can choose 000, 001, 010, 001, 101, 011: 000 coressponds to emty, 010 to 7, 101 to 5 + 3 and so on).
For each state and mask we need to iterate over all submasks and we can do it efficiently in the way it is shown in code. It can be proven, that time complexity of this code is O(m*3^m), space complexity is O(m*2^m).
class Solution:
def canDistribute(self, a, customers):
m = len(customers)
a = sorted(Counter(a).values())[-m:]
n = len(a)
mask_sum = [0]*(1<<m)
for mask, i in product(range(1<<m), range(m)):
if (1 << i) & mask:
mask_sum[mask] += customers[i]
@lru_cache(None)
def dfs(i, mask):
if mask == 0: return True
if i == n: return False
submask = mask
while submask:
if mask_sum[submask] <= a[i] and dfs(i+1, mask ^ submask):
return True
submask = (submask-1) & mask
return dfs(i+1, mask)
return dfs(0, (1<<m) - 1)
Problem 1659 Maximize Grid Happiness
https://leetcode.com/problems/maximize-grid-happiness/
Let us us dynamic programming with the following states:
index: number of cell in our grid, going from0tomn-1: from top left corner, line by line.rowis the next row filled with elements0,1(for introvert) or2(for extravert): see on my diagramm.Iis number of interverts we have left.Eis number of extraverts we have left.
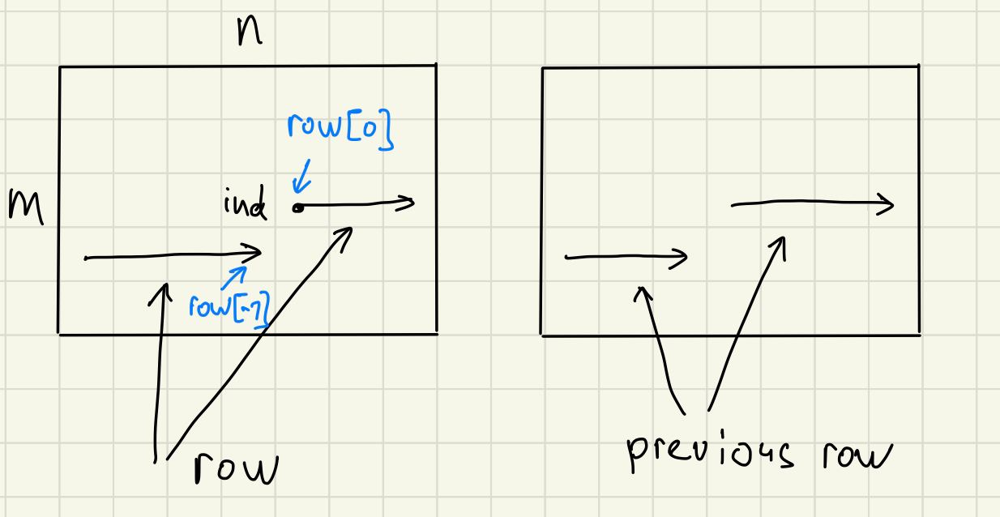
Now, let us fill out table element by element, using dp function:
- First of all, if we reached
index == -1, we return 0, it is our border case. - Compute
RandCcoordinates of our cell. - Define
neibs: it is parameters for our recursion: fist element is what we put into this element:0,1or2, second and third elements are new coordinates and last one is gain. - Now, we have
3possible cases we need to cover: new cell is filled with0,1or2and for each of these cases we need to calculateans:
a) this isdpfor our previous row, shifted by one
b) gain we need to add when we add new intravert / extravert / empty
c) check right neighbor (if we have any) and addfine: for example if we have 2 introverts, both of them are not happy, so we need to add-30-30, if we have one introvert and one extravert, it is20-30and if it is two extraverts it is20+20.
d) do the same for down neigbor if we have any (see illustration for help)
Finally, we just return dp(m*n-1, tuple([0]*n), I, E)
Complexity: time complexity is O(m*n*I*E*3^n), because: index goes from 0 to mn-1, row has n elements, each of them equal to 0, 1 or 2.
class Solution:
def getMaxGridHappiness(self, m, n, I, E):
InG, ExG, InL, ExL = 120, 40, -30, 20
fine = [[0, 0, 0], [0, 2*InL, InL+ExL], [0, InL+ExL, 2*ExL]]
@lru_cache(None)
def dp(index, row, I, E):
if index == -1: return 0
R, C, ans = index//n, index%n, []
neibs = [(1, I-1, E, InG), (2, I, E-1, ExG), (0, I, E, 0)]
for val, dx, dy, gain in neibs:
tmp = 0
if dx >= 0 and dy >= 0:
tmp = dp(index-1, (val,) + row[:-1], dx, dy) + gain
if C < n-1: tmp += fine[val][row[0]] #right neighbor
if R < m-1: tmp += fine[val][row[-1]] #down neighbor
ans.append(tmp)
return max(ans)
if m < n: m, n = n, m
return dp(m*n-1, tuple([0]*n), I, E)
Problem 1681. Minimum Incompatibility
https://leetcode.com/problems/minimum-incompatibility/
We need to keep state in the form: bitmask, last, where:
bitmaskis bitmask for all numbers already taken.lastis index of last taken number.
How are we going to form our groups: sort our numbers first and imagine we have numbers [1,1,2,3,3,4]: and k = 3. Then we need to create first group of 2 elements, for example it can be elements with indexes 1,2, and we have current bitmask 011000, then we need to form another group of 2 elements, for example it can be elements with indexes 0,5, so we have bitmask 111001 now. Finally we put last two elements in last group. We can interpret it as TSP problem: we choose path 1->2->0->5->3->4. Note, that in each group we only choose increasing indexes, whereas between groups than can decrease (but can increase also).
Now, what we have in our algorithm:
- We iterate over all possible
mask - Calculate places, where we have
1in this mask. - Now, we can have two cases: first, if
len(n_z_bits)%(n//k) == 1: it means, that it is time to start new group, so we can choose any index we want, not neccecerily bigger than previous, so we choosepermutationshere: there will be exactlyt(t-1)/2pairs and for each of them we updatedp[mask][l]. - In other case, it means, that we need to continue to build our group, so next index should be bigger than previous and we choose
combinationshere. Also we check that new number is not equal to last one we have and again updatedp[mask][l]. - Finally, we return minimum from
dp[-1].
Complexity: time complexity is O(n*n*2^n) as TSP have: we have 2^n bitmasks and we have O(n^2) time to process each mask. In python it is working not very fast, I can say it is barely accepted, so, I think there should be O(n*2^n) solution as well, if you know such solution (desirebly with explanations), please let me know!
class Solution:
def minimumIncompatibility(self, nums, k):
n = len(nums)
if k == n: return 0
dp = [[float("inf")] * n for _ in range(1<<n)]
nums.sort()
for i in range(n): dp[1<<i][i] = 0
for mask in range(1<<n):
n_z_bits = [j for j in range(n) if mask&(1<<j)]
if len(n_z_bits)%(n//k) == 1:
for j, l in permutations(n_z_bits, 2):
dp[mask][l] = min(dp[mask][l], dp[mask^(1<<l)][j])
else:
for j, l in combinations(n_z_bits, 2):
if nums[j] != nums[l]:
dp[mask][j] = min(dp[mask][j], dp[mask^(1<<j)][l] + nums[l] - nums[j])
return min(dp[-1]) if min(dp[-1]) != float("inf") else -1
Problem 854 K-Similar Strings
https://leetcode.com/problems/k-similar-strings/
Note similarity of this problem with Problem Q765 Couples Holding Hands, but here we have more 6 different symbols. Let us look at this problem as to graph: for example if we have A = abcde and B = bcaed, then we need to find 2 loops: a -> b -> c -> a and d -> e -> d. In general we need to find minimum number of loops in directed graph on m = 6 nodes, where we can have multiple edges and we have n edges. However it is still difficult problem and it is not obvious how to handle it.
Let us assign number to each letter: a:1, b:32, c:32^2, d:32^3, e:32^4, f:32^5. Now, we evaluate difference between corresponding elements of two strings, so for example for given example we have [-31, -992, 1023, -1015808, 1015808]. Now, finding loop is equivalent to group of elements which has 0 when we sum them! Why? Because if some sum is equal to zero, it means, that numbers in both sets are equal: we choose 32 > 20, length of our string): indeed, imagine, that we have set of numbers with sum $0$, it means:
alpha_0 * 1 + alpha_1 * 32 + ... + alpha_5 * 32^5 = beta_0 * 1 + beta * 32 + ... + beta * 32^5,
where alpha_0, ... alpha_5 is corresponding number of a, b, c, d, e, f, similar for betas. From here we have
gamma_0 * 1 + gamma_1 * 32 + ... + gamma_5 * 32^5 = 0,
where gamma_i = alpha_i - beta_i lies in [-20, 20]. If we consider biggest gamma_i which is not equal to 0, then sum of all other terms is smaller than this term, so it means that all gamma_i equal to zero, that is we have the same set of letters.
Actually, this is almost equivalent to Problem Q698 Partition to K Equal Sum Subsets we already discussed. Time complexity is O(2^n * n) and space complexity is O(2^n).
To be accepted on Leetcode, we need to make couple of optimizations: first of all, if two symbols on the same place are equal, we just remove them. Also if we have loop of length 2 we also remove it: here I use trick, where we intersect count for nums and list with all opposite numbers from nums. Then for each element we repeat it as much times as needed and delete from our list.
class Solution:
def kSimilarity(self, A, B):
nums = [((1<<ord(i)*5) - (1<<ord(j)*5))>>(97*5) for i,j in zip(A,B) if i!=j]
Cnt = Counter(nums) & Counter(-n for n in nums)
pairs = list(chain(*([i]*j for i, j in Cnt.items())))
for num in pairs: nums.remove(num)
n = len(nums)
dp = [(-1,0)] * (1<<n)
dp[0] = (0, 0)
for mask in range(1<<n):
for j in range(n):
if mask & (1<<j):
steps, summ = dp[mask ^ (1<<j)]
dp[mask] = max(dp[mask], (steps + (summ==0), summ + nums[j]))
return n - dp[-1][0] + len(pairs)//2
Problem 1799 Maximize Score After N Operations
https://leetcode.com/problems/maximize-score-after-n-operations/
Let us define by dp(bitmask) the answer for subproblem, where we can use only numbers with 1 bits, for example if nums = [1,2,3,4,5,6] and bitmask = 010111, we can use numbers 2, 4, 5, 6.
How we can calculate dp(bitmask)? We need to look at all pairs of not used yet numbers and take dp of the resulting mask. Then choose maximum among all possible candidates.
Complexity: time complexity is O(2^(2n)*n^2), because we have 2^(2n) different bitmasks and for each masks and for each of them we have O(n^2) transitions to other bitmasks. Also I precalculated all gcds, which will give you complexity O(n^2*log M), where M is the biggest number in nums. Space complexity is O(2^(2n)).
class Solution:
def maxScore(self, nums):
n = len(nums)
gcds = {(j, k): gcd(nums[j], nums[k]) for j, k in combinations(range(n), 2)}
@lru_cache(None)
def dfs(bitmask):
if bitmask == 0: return 0
cand = 0
n_z_bits = [j for j in range(n) if bitmask&(1<<j)]
for j, k in combinations(n_z_bits, 2):
q = bitmask^(1<<j)^(1<<k)
cand = max(cand, dfs(q) + (n+2 - len(n_z_bits))//2*gcds[j, k])
return cand
return dfs((1<<n) - 1)
If you know more problems where you can use dp on subsets, please let me know in comments, I will add it (probably some of the premium problems are, but I do not have access to them, also I did not solve all problems on leetcode, so I probably missed some of the problems)
Problem 1879 Minimum XOR Sum of Two Arrays
https://leetcode.com/problems/minimum-xor-sum-of-two-arrays/
Here we briefly talk about solution. Let us go from left to right on array A and allocate elements to A[0], then to A[1] and so on. We have two pieces of information in our dp function:
maskis binary mask of unused elements fromB. For example if we have01001, it means that we still can use element with index0and element with index3.iis current index inA. Actually, it can be computed from bitmask: how manynon-zerobits we have in it. But it is more simple to keep it as well.
Finally, what we do is just try to allocate already not used elements and run function recursilvey, that is all!
Why I spend 1 hour to find my mistake? It is all about bitwise operations: you NEED BRACKETS in (A[i]^B[j]), in the opposite case it will not work.
Complexity:
Time complexity is O(n*2^n), because we have 2^n states and O(n) transactions frome one state to others. Space complexity is O(2^n).
class Solution:
def minimumXORSum(self, A, B):
n = len(A)
@lru_cache(None)
def dp(mask, i):
if i == n: return 0
return min(dp(mask ^ (1<<j), i + 1) + (A[i]^B[j]) for j in range(n) if mask & 1<<j)
return dp((1<<n) - 1, 0)
1349. Maximum Students Taking Exam
https://leetcode.com/problems/maximum-students-taking-exam/
Solution 1
First solution idea is to fill line by line and make sure that we do not have any collisions between line. What we can do is for every line (row) compute all possible patterns for this row first. Then we will use function dp(curr, i), where:
curris bitmask for the current row we are now.iis number of current row.
Then to evaluate dp(curr, i), we need to look at all rows from masks[i-1] and make sure that we do not have a collision: we already checked that we do not have any in each row, it is enough the check that we do not have between rows, we can do it, using if not (curr >> 1) & prev and not curr & (prev >> 1) condition: we move one of the rows to the left and check if we have ones at the same place.
Complexity
Rude estimate is O(2^n * 2^n * m), because we have 2^n * m different states and O(2^n) transitions from one state to others. Space complexity is O(2^n * m). In fact, there will be no more than O(phi^n) states for each row (where phi approximately 1.6 is golden ratio), so final time complexity can be estimated as O(phi^{2n} * m), space complexity is O(phi^n * m).
Code
class Solution:
def maxStudents(self, seats):
m, n = len(seats), len(seats[0])
masks = []
for row in seats:
mask = sum((1 << j)*(v==".") for j, v in enumerate(row))
masks.append([i for i in range(1<<n) if i & mask == i and not i & (i>>1)])
@lru_cache(None)
def dp(curr, i):
if i == -1: return 0
res = 0
for prev in masks[i-1]:
if not (curr >> 1) & prev and not curr & (prev >> 1):
res = max(res, dp(prev, i - 1))
return res + bin(curr).count("1")
return max(dfs(mask, m-1) for mask in masks[m-1])
Solution 2
There is smarter solution, using idea of dp with broken profile, see also similar problem 1659.
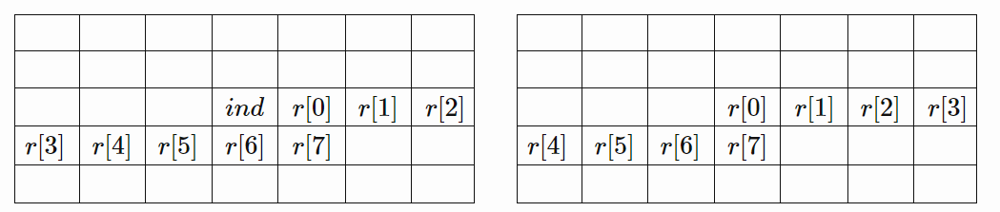
Here we need to keep broken row with total n+1 elements. Now, we can try to fill element in index place either with 0 or with 1. We always have option to put 0. If we want to put 1 we need to make sure, that we do not have conflict:
- We need to make sure, that if we have neighbour to the right, then value of this element is not equal to
1: first bit ofrowcan be taken withrow & (1<<n)formula. - We need to make sure, that if we have neighbour to the right bottom, then its value is not equal to
1. To get this element we can userow & 1, which will give the last bit ofrow. - We need to make sure, that if we have neighbour to the left bottom, then its value is not equal to
1. To get this element we need to takerow & 4, that is the 3-rd element from the end ofrow. - Finally, we need to make sure, that
S[y][x]is not equal to#.
In the end we return dp(m*n-1, 0).
Complexity
We can estimate number of states as O(mn* 2^{n+1}, and we have 2 transactions from one state to another. Hence time and space complexity is O(mn* 2^n). It can be shown that in fact it is O(mn* phi^n).
Code
class Solution:
def maxStudents(self, S):
m, n = len(S), len(S[0])
@lru_cache(None)
def dp(index, row):
if index == -1: return 0
y, x = index//n, index%n
c = (x < n-1 and row & 1<<n) or (x < n-1 and y < m-1 and row & 1)
c = c or (x > 0 and y < m-1 and row & 4) or (S[y][x] == "#")
cands = [dp(index-1, row//2)]
if not c: cands.append(1 + dp(index-1, row//2 + (1<<n)))
return max(cands)
return dp(m*n-1, 0)
Remark
There is in fact O(m^2 n^2) time complexity algorithm for this problem, because our graph in fact bipartite: odd and even columns can be seen as two parts of our graph and the question is to find maximum independent set in this graph.
Problem 1125. Smallest Sufficient Team
https://leetcode.com/problems/smallest-sufficient-team/
Solution 1
Let dp(i, mask) is minimum number of people needed to cover bitmask mask if we already covered i persons. In fact we will keep two values: (minimum number of people, last taken).
- First we need to create
masks: set of skils for each person - If
i == -1, andmask = 0, we return(0, -1), it means that wedo not use any person yet and-1means that we reached the bottom. Ifi == -1andmask != 0, we return(inf, -1), it means that we reached bottom but did not covered all skills. - Finally, we have two choices: either take person
ior do not take it. Heremask & ~masks[i]is used for subtraction of sets. - In the end use backtracking to create solution.
Complexity
Time and space complexity is O(k*2^n). Space complexity can be reduced to O(2^n).
Code
class Solution:
def smallestSufficientTeam(self, req_skills, people):
d = {s:i for i, s in enumerate(req_skills)}
masks = [sum(1<<d[skill] for skill in p) for p in people]
n, k = len(req_skills), len(people)
@lru_cache(None)
def dp(i, mask):
if i == -1: return (mask*1000, -1)
cand1 = dp(i-1, mask)
cand2 = (dp(i-1, mask & ~masks[i])[0] + 1, i)
return min(cand1, cand2)
mask, ans = (1<<n) - 1, []
while mask:
steps, last = dp(k - 1, mask)
ans.append(last)
mask &= ~masks[last]
return ans
Solution 2
Actually, we can write it in more shorter way if we keep not the last person used, but bitmask of used one (we have at most 60, so it will fit in long not only in python)
Complexity
It is the same as in previous approach.
Solution
class Solution:
def smallestSufficientTeam(self, req_skills, people):
d = {s:i for i, s in enumerate(req_skills)}
masks = [sum(1<<d[s] for s in p) for p in people]
n, k = len(req_skills), len(people)
@lru_cache(None)
def dp(i, mask):
if i == -1: return (mask*1000, 0)
steps, peop = dp(i-1, mask & ~masks[i])
return min(dp(i-1, mask), (steps + 1, peop + (1<<i)))
M = dp(k - 1, (1<<n) - 1)[1]
return [i for i in range(k) if M & (1<<i) != 0]
If you have any question, feel free to ask. If you like the explanations, please Upvote!
May 31, 2021 10:27 PM
Here are a few more bitmask dp problems:
https://leetcode.com/problems/maximum-number-of-groups-getting-fresh-donuts/
https://leetcode.com/problems/maximum-students-taking-exam/
Let's keep this list going!
March 24, 2021 4:43 PM
for example 00011101 mask means that we use nodes number 0, 2, 3, 4. can someone please explain what this means?
May 30, 2021 11:17 PM
Spasibo Dmitry.
Thank you (I doubt a key chain will be enough to properly reward this post).
I recently came across "1799. Maximize Score After N Operations" which can be solved this way too. I didn't know it was named "DP on subsets".
Thanks a lot!
It is a very useful bunch of problems discussed. It is much clearer now.
March 25, 2021 1:03 AM
Awesome, thanks!
hi, one question, what is the meaning of neib variable in the first 2 problems ?


