210 course schedule II

Here is my discussion post.

It is challenge for me to master a graph algorithm. I plan to spend time to review my practice back in February, 2017 first. I like to share my practice and will work on new version very soon.

Case study example graph
Example 2:

Input: 4, [[1,0],[2,0],[3,1],[3,2]]
Output: [0,1,2,3] or [0,2,1,3]

In order to understand graph, how to apply topological sort, we have to understand the dependency stored in the array, [1,0] tells us that course 0 should be taken first then course 1 can be taken. likewise, we can interpret [2,0],[3,1],[3,2].

Let me draw the tree based on the above dependency, the graph can be very helpful to understand how to approach the problem using topological sorting; even if I forget the algorithm, I still can figure out the reasonable order based on those prerequisite courses.

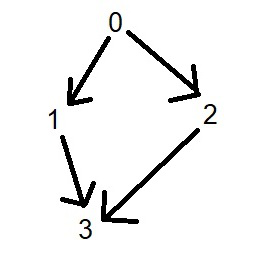
The most challenge part is design decision. How to represent the graph using data structures? We can name the node using index = 0, 1, ...n, and each node ( course) has dependents; so the course can be prerequisite course for others, it can be stored in a stack, and then each course has indgree ( the concept is prerequisite courses) value.
So declaration statements are the following:
var dependents = new Stack[numCourses];
var indegree = new int[numCourses];

The output of courses taken in order is stored in integer array.

Build the graph by going over each entry in matrix.
Next step is to add those courses into queue with 0 indegree. Take those course first, and then update indegree for each course if related.

Here are highlights:

1. Build a graph using selected data structures, indegree, dependency list;
2. Start to do BFS search using Queue, add those indegree courses to the queue;
3. Do not forget to update indegree count after the course is ready to take based on indegree value 0;
4. Work on example graph if there is problem in thinking process. Be patient! Example graph, take course 0, next step take 1 or 2, and then take one from 1 or 2 if it is not taken before, and last step take course 3.

public class Solution {
    public int[] FindOrder(int numCourses, int[,] prerequisites) {
         var dependents = new Stack<int>[numCourses];

            for (int i = 0; i < numCourses; ++i)
            {
                dependents[i] = new Stack<int>();  
            }

            // build dependency list for each prerequisite course, 
            // and set up indegree variable for each courses matching with prerequisite courses' number.
            int[] indegree = new int[numCourses];
            for (int i = 0; i < prerequisites.GetLength(0); ++i)
            {
                int takeFirst = prerequisites[i, 1];
                int takeAfter = prerequisites[i, 0];

                dependents[takeFirst].Push(takeAfter); 
                ++indegree[takeAfter];             
            }

            // add those courses with 0 indegree to the queue
            Queue<int> queue = new Queue<int>();
            for (int courseId = 0; courseId < numCourses; ++courseId)
            {
                if (indegree[courseId] == 0)
                {
                    queue.Enqueue(courseId);
                }
            }

            // take courses with indgree zero only
            var coursesByTakingOrder = new int[numCourses];
            int count = 0;
            while (queue.Count > 0)
            {                   
                int readyToTake = queue.Dequeue();

                coursesByTakingOrder[count++] = readyToTake;   

                foreach (int courseId in dependents[readyToTake])
                {
                    // decrement value of indegree by 1 
                    indegree[courseId]--;

                    // add to the queue if there is no prerequisite left
                    if (indegree[courseId] == 0)   
                    {
                        queue.Enqueue(courseId);
                    }
                }
            }

            if (count != numCourses)
            {   
                return new int[]{}; 
            }

            return coursesByTakingOrder;
    }
}