1049. Last Stone Weight II

Oct. 9, 2019

Introduction

It is the algorithm for me to practice dynamic programming, and also it can be converted into classical algorithm called Knapsack algorithm. I had to spend extra few hours to study and then figure out the solution with more detail.

Case study

I added one more case study, and then look into challenge to prevent one stone to be counted more than once in any sum.

Here is my post.

Oct. 8, 2019 9:11 PM
It is the first submission I made by studying one of solutions written in Chinese. I still have several concerns in terms of implementation.

In order to fully understand the algorithm, I asked myself why the second for loop is looping from sum/2 to current variable value, can we do increasing order from current variable value to sum/2 instead. I changed the code, and then one of test cases fails.

I need to look into and be able to explain the above failed test case to change for loop from decreasing order to increasing order. I need to ask a few questions, and work on basics first.

I will come back and update the post based on better understanding of the algorithm.

Follow up on Oct. 9, 2019

I have to answer two questions in my knapsack solution, and argue that why my approach is correct.
Question 1:
The order does not matter. In my C# code, for (int i = 0; i < length; i++) , any order will work. Why?
Question 2:
In my C# code,for (int j = sum / 2; j >= current; j--), why it has to be in descending order in your for loop? Can we use ascending order from current to sum /2.
I think that if I can answer those two questions, I prove that I have a good understanding of my reasoning. Otherwise I just try to pass online judge, I studied the code but I could not figure out the same day.

My argument to answer the question 2 is that every stone can only be used once. So it has to be in descending order, otherwise one stone may be counted more than once to sum value.
My argument to answer the question 1 is hard to describe. I have to prove it using a generic case, give any sum = s1 + s2 + ... + si, each stone in right hand side will be consider once, and then assuming that 1, 2, ..., i is the order to show in the array, and then s1 will be marked true, next s1 + s2, ..., s1 + s2 + ...+si = sum is marked as true. That is all.

I also asked the question in the most popular discussion post here.

Follow up
Case study
In order to fully understand the algorithm, I asked myself why the second for loop is looping from sum/2 to current variable value, can we do increasing order from current variable value to sum/2 instead. I changed the code, and then one of test cases fails.
for (int j = sum / 2; j >= current; j--) => for (int j = current; j <= sum / 2; j++)

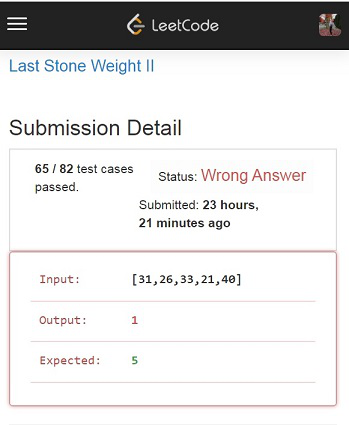
Given the array with values [31, 26, 33, 21, 40], the sum of the array is 151, let us denote it as Sum. Sum/ 2 will be 75. We can divide into two sets, [33, 40] and [31, 26, 21], the sum of first array is 73, and the sum of second array is 78, the minimum difference is 5.

But if we update the loop from ascending, one number may be used more than once, so that minimum difference can be one. Since [26, 26, 23] can be an array, but 26 is counted twice, the sum of the array is 75, so 151 - 2 * 75 = 1.

The following code passes online judge.

public class Solution {
    /// <summary>
        /// study code
        /// https://www.acwing.com/solution/LeetCode/content/2139/
        /// I like to read comment written in Chinese. I like to write good comment like this 
        /// as well one day. 
        /// (动态规划) O(n×sum)
        /// 合并的过程就是给每个重量前赋值正号或者负号的过程，相当于把这些石头分为两组，
        /// 使得两组的差值尽可能小，所以这是经典的集合划分NP完全问题，可以采用动态规划的方法求解。
        /// 设状态 f(i) 表示是否存在一个划分，使得某组的重量综合为 ii。
        /// 初始时 f(0)=true，其余为 false。
        /// 转移时，模仿01背包的算法，对于每个物品，有放和不放两种决策，故 
        /// f(j)=f(j)|f(j−stones[j])。
        /// 最终答案需要枚举，j 从 sum/2 开始到 0，如果 f(j)==true，则返回 sum−j−j。
        /// 时间复杂度
        /// 状态数为 O(n×sum)，转移数为常数，故时间复杂度为 O(n×sum)。
        /// 空间复杂度
        /// 需要额外 O(n) 的空间构造堆。
        /// </summary>
        /// <param name="stones"></param>
        /// <returns></returns>
        public int LastStoneWeightII(int[] stones)
        {
            var length = stones.Length;
            var sum = stones.Sum();

            var found = new bool[sum + 1];
            found[0] = true;

            // transition formula - figure out the reasoning later
            for (int i = 0; i < length; i++)
            {
                var current = stones[i];
                for (int j = sum / 2; j >= current; j--)
                {
                    found[j] = found[j] | found[j - current];
                }
            }

            // Find maximum sum less and equal to sum/2. 
            for (int i = sum / 2; i >= 0; i--)
            {
                if (found[i])
                {
                    return sum - i - i; 
                }
            }

            return sum; 
        }
}