Here is the link.
C# | Quick learner | 3+ solutions | recursive function | stack | Morris traversal
August 23, 2022
I like to review C# solutions in discuss post, and then write a solution using recursive, a stack, and a solution without using recursive or stack - using Morris order traversal. The time complexity is O(N), N is total number of nodes in the tree, space optimal is O(1) using Morris order traversal.
The following are 4 solutions I like to share.
Solution 1:
I choose to use C# List and also write a function to pass List as a function argument, so all nodes in the tree will be visited once and be added to List in inorder traversal order.
Space complexity: Using O(N) space, List
Time complexity: O(N), N is the total number of nodes in the tree
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _94_inorder_traversal
{
class Program
{
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
this.val = val;
this.left = left;
this.right = right;
}
}
static void Main(string[] args)
{
var root = new TreeNode(1);
root.right = new TreeNode(2);
root.right.left = new TreeNode(3);
var list = InorderTraversal(root);
Debug.Assert(string.Join(",", list).CompareTo("1,3,2") == 0);
}
/// <summary>
/// emtpy tree, with one root node, with more nodes
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public static IList<int> InorderTraversal(TreeNode root)
{
var list = new List<int>();
runInorderTraversal(root, list);
return list;
}
private static void runInorderTraversal(TreeNode root, IList<int> list)
{
if (root == null)
{
return;
}
runInorderTraversal(root.left, list);
list.Add(root.val);
runInorderTraversal(root.right, list);
}
}
}
Solution 2 | Using stack | iterative solution
I think that the design should be simple. Go over a few test cases, and then complete the design.
Here are highlights for a good and simple design using a stack:
- Inorder traversal - left child, root node, right child
- Use stack to maintain the order, allow left child pop out first before root node - reverse the order
- Design an algorithm using stack, using a stack, a variable called TreeNode current
- Make sure that stack.Push, stack.Pop both are called once
- Design two nested while loop - outside while loop is to work on the root node, inside while loop is to work on root node -> left child until the end
- Choose a simple test case to work on first: A root node with value 1, which has a left child with value 2; and root.left has a left child with value 3 - using the test case to work on inside while loop functionality.
- The above 6 steps should be a good start to make a working solution.
The following C# code passes online judge.
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _94_inorder_traversal_iterative
{
class Program
{
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null)
{
this.val = val;
this.left = left;
this.right = right;
}
}
static void Main(string[] args)
{
var root = new TreeNode(1);
root.right = new TreeNode(2);
root.right.left = new TreeNode(3);
var list = InorderTraversal(root);
Debug.Assert(string.Join(",", list).CompareTo("1,3,2") == 0);
}
/// <summary>
/// study code
///
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public static IList<int> InorderTraversal(TreeNode root)
{
var list = new List<int>();
if (root == null)
{
return list;
}
// stack - inorder - left, root, right
var stack = new Stack<TreeNode>();
var current = root;
// stack
// design - visit left child and right child at least once
// put left child first, before root node itself.
// stack.Push - only once - in coding writing
// stack.Pop - only once - in coding writing
//
while (stack.Count > 0 || current != null)
{
// Go over an example
// Binary tree - Test case 1:
// root = new TreeNode(1);
// root.left = new TreeNode(2);
// root.left.left = new TreeNode(3);
// nodes should be pushed into stack: push 1, push 2, push 3
// Work on test case 1, and then add a right node into tree, work on test case 2 to cover all test cases.
while (current != null)
{
stack.Push(current);
current = current.left;
}
// Pop()
current = stack.Pop();
list.Add(current.val);
// Go to right
current = current.right;
}
return list;
}
}
}
Solution 3: Morris traversal | O(N) time, O(1) space | Space optimal
Morris (InOrder) traversal is a tree traversal algorithm that does not employ the use of recursion or a stack. In this traversal, links are created as successors and nodes are printed using these links. Finally, the changes are reverted back to restore the original tree.
10 minutes to review the algorithm
Morris traversal Algorithm
- Initialize the root as the current node curr.
- While curr is not NULL, check if curr has a left child.
- If curr does not have a left child, print curr and update it to point to the node on the right of curr.
- Else, make curr the right child of the rightmost node in curr's left subtree.
- Update curr to this left node.
Illustration | Demo | https://www.educative.io/answers/what-is-morris-traversal
It is a good investment to spend 10 minutes to go over a demo before spending time to read C# solution.
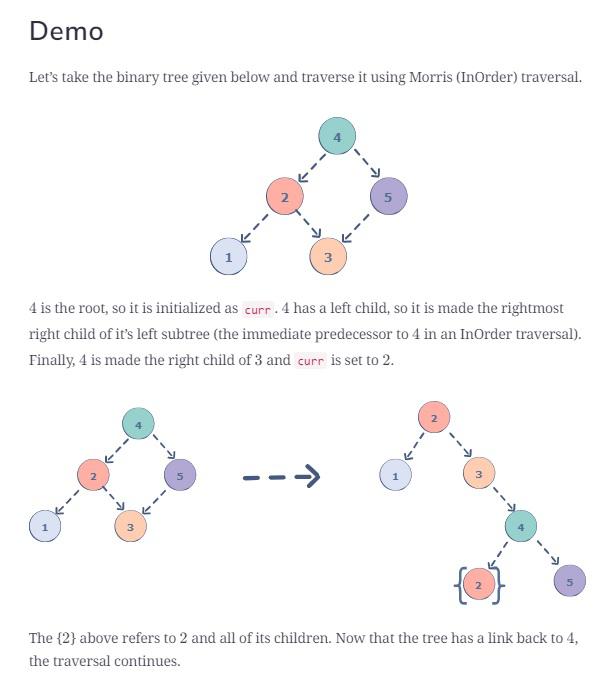
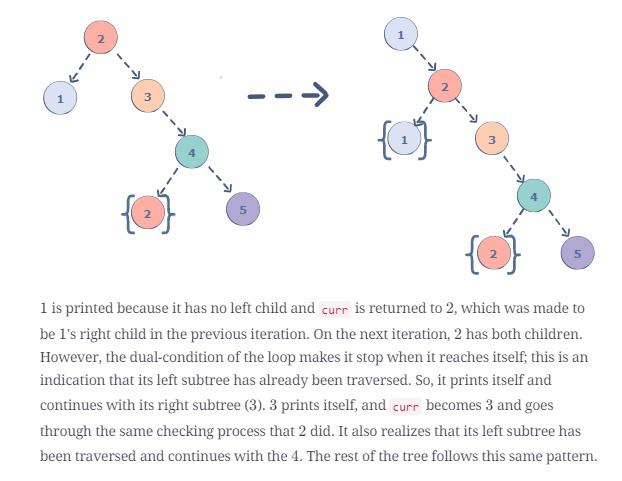
Test cases | Debugging | Tree restored | First node 1 in inorder | Second node 2 in inorder
It is definitely a good exercise to run the debugger, and then track the demo tree first node with value 1 in inorder traversal, and then second node with value 2 in inorder traversal. Rest should be easy. I found out that it is so interesting for me to learn this Morris order traversal with this demo tree.
The following C# code passes online judge.
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _94_inorder_traversal
{
class Program
{
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null)
{
this.val = val;
this.left = left;
this.right = right;
}
}
static void Main(string[] args)
{
var root = new TreeNode(4);
root.left = new TreeNode(2);
root.right = new TreeNode(5);
root.left.left = new TreeNode(1);
root.left.right = new TreeNode(3);
var list = InorderTraversal(root);
Debug.Assert(string.Join(",", list).CompareTo("1,2,3,4,5") == 0);
}
/// <summary>
/// study code
/// This is C# implementation with Morris In-Order traversal.
/// Time complexity is O(n)
/// Space complexity is O(1)
/// https://leetcode.com/problems/binary-tree-inorder-traversal/discuss/441037/C-Morris-InOrder-Traversal
/// study Morris traversal
/// https://www.educative.io/answers/what-is-morris-traversal
/// Morris (InOrder) traversal is a tree traversal algorithm that does not employ
/// the use of recursion or a stack. In this traversal, links are created as successors
/// and nodes are printed using these links. Finally, the changes are reverted back to
/// restore the original tree.
/// </summary>
/// <param name="root"></param>
/// <returns></returns>
public static IList<int> InorderTraversal(TreeNode root)
{
var result = new List<int>();
if (root == null)
{
return result;
}
var current = root;
while (current != null)
{
if (current.left == null)
{
result.Add(current.val);
current = current.right;
}
else
{
// make the current node the right child of the rightmost node in curr's left subtree
// illustration please the diagram
//
// find the predec of current
var previous = current.left;
while (previous.right != null && previous.right != current)
{
previous = previous.right;
}
if (previous.right == null)
{
previous.right = current; // node 3.right = node 4
current = current.left; //
}
else
{
previous.right = null;
result.Add(current.val); // demo tree - first time, node 2 is node 1's right child
current = current.right;
}
}
}
return result;
}
}
}
Solution 4 | Need improvement | Weakness in design
Oct. 4, 2018
It is a medium level tree algorithm. I submitted the solution more than four months ago. I like to review the code before I start to work on other 20 medium level tree algorithms. It is also a good idea to share here.
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public IList<int> InorderTraversal(TreeNode root) // emtpy tree, with one root node, with more nodes
{
if (root == null)
{
return new List<int>();
}
var left = InorderTraversal(root.left);
left.Add(root.val);
var right = InorderTraversal(root.right);
// add right to left list <- code review on August 23, 2022, it is not a good practice.
if (right.Count > 0)
{
foreach (var item in right)
{
left.Add(item);
}
}
return left;
}
}
I think that it is better to avoid copying the list from right variable to left. It takes extra time and no need to do that.
No comments:
Post a Comment