Leetcode discuss: 1080 Insufficient Nodes in Root to Leaf Paths

Here is the link.

C# Simple solution using post order traversal

July 11, 2020

1080. Insufficient Nodes in Root to Leaf Paths

Introduction

I only have one week to prepare for Facebook phone screen on July 20, 2020. I found out that I did not learn very well last 12 months on this tree algorithm, first practice was in mock interview on June 8, 2019, but I did not solve the problem; second practice was on July 10, 2020, it took me 85 minutes.

Case study

I like to walk through three test cases with the following simple solution, explain to myself how it works.

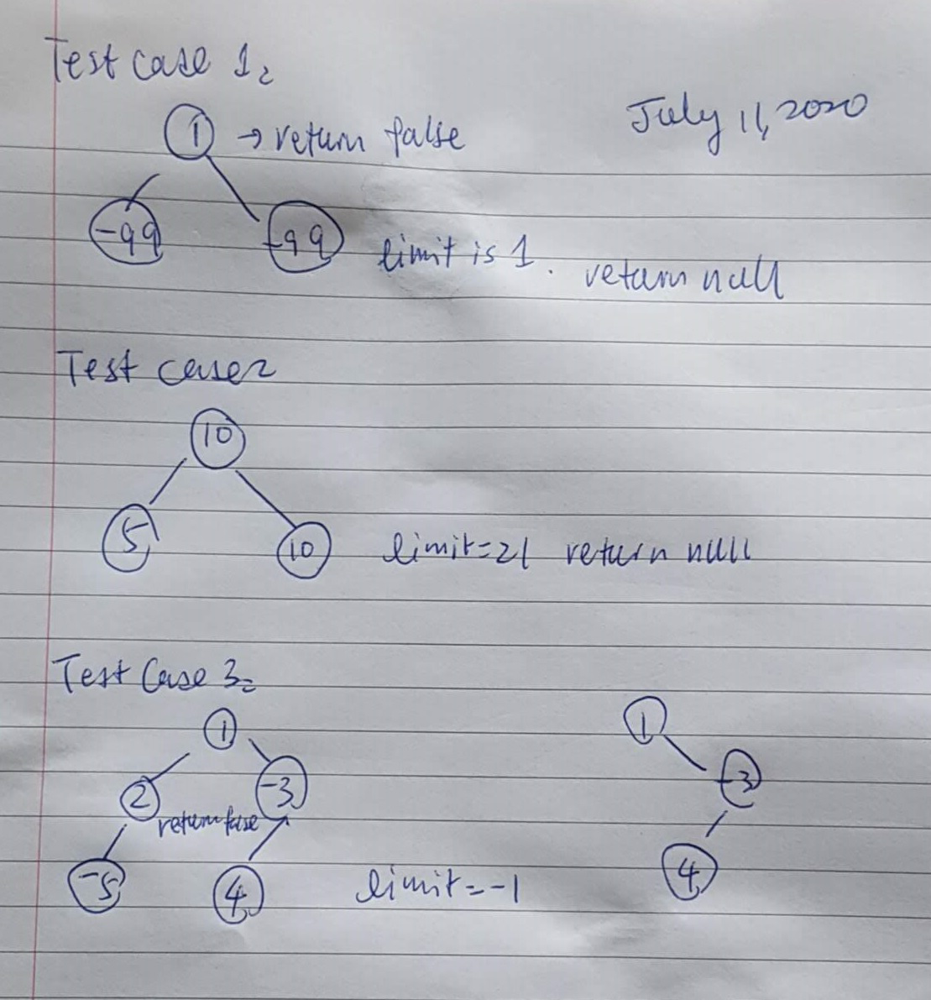
Lower my target when I work on analysis and coding, try to walk through those three test cases, make sure that they all working properly.

Try to simplify the solution, solve it in less than 20 minutes.

Five things - make sure five statements are not missing

1. root to node p's path sum comparison to limit value - target;
2. Step 1 more detail, the checking is delayed until the child's recursive call; Leaf node will add its value to sum, and pass the sum to children's recursive call;
3. Add root node's val to sum variable
4. Post order traversal - so the node can determine if it should stay or be removed
5. Remove left child or right child
6. Return true of false to parent call in call stack

Most challenge - recursive function design - what to return?

The post order traversal return with a bool value, and here are definitions for various cases:

1. If it is empty left or right child of leaf node, then check sum with root to leaf node path sum;
2. If it is not a leaf node, then one of chilren has a leaf to survive, return true, otherwise return false;
3. The node will check it's left and right child return, if left child recursive call returns false, then remove left child, same as right child.
4. Think about this recursive design using a bool, how many roles it can help to play.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public TreeNode SufficientSubset(TreeNode root, int limit) {
        if(root == null)
        {
            return null;
        }
        
        if(postOrderTraversal(root,limit,0))
        {
            return root;
        }        
        else
        {
            return null;
        }
    }
    
    /// take some risk
    /// make code simple
    /// if the node is the leaf node of original tree before nodes are removed,
    ///  compare sum with target; only compare when it is leaf node
    /// else 
    ///  post order traversal - a node without any children may not be leaf node
    //   check it's left and right return
    public bool postOrderTraversal(TreeNode node,int target,int sum)
    {
        if(node == null)
        {
            return sum >= target;
        }
        
        sum += node.val;
        
        var left  = postOrderTraversal(node.left, target,sum);
        var right = postOrderTraversal(node.right,target,sum);
        
        if(!left)
        {
            node.left = null;
        }
        
        if(!right)
        {
            node.right = null;
        }
        
        if(node.left == null && node.right == null)
        {
       // test case 1: this applies to three node in the tree, 
    //   bottom up, 
    //   first one: -99 left, second one: -99 right, last one: 1 root
    // test case 3: Only apply to three nodes, node 4 and node -5, node 2
    // leaf node 4, return true & true
    // leaf node -5, return false & false
    // node 2, return false
            return left & right;
        }
        else
        {
      // test case 3: root node 1
            return true;
        }
    }    
}