Leetcode discuss: 889. Construct Binary Tree from Preorder and Postorder Traversal

 Here is the link. 

C# Construct tree using preorder traversal first

August 30, 2020
889. Construct Binary Tree from Preorder and Postorder Traversal
Introduction
I like to learn all ideas to solve this tree algorithm. I came cross this idea from the discussion post here.

The idea is to construct binary tree using preorder traversal list, so it is easy to figure out the order of nodes in preorder list is from root node to left child until last one without left child. And then it is time to set up a node as a right child.

Case study
I like to draw the diagram to explain how to solve this question using given example in the problem statement.
Input: pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
Output: [1,2,3,4,5,6,7]

I debugged the code and then figured out the idea. It is to construct binary tree using preorder list first, starting from root node, and then go left continuously until it is the node without left child. Actually it is the first node in postorder traveral.

Using the example, root node 1 -> left child - node 2 -> left child - node 4, argue that it is the node without left child, since value is the first node in postorder traversal, marking using a in the following diagram. Preorder traversal list is iterated from a to b to c, the third node is with value 4. Now need to increment postorder traversal list's index.

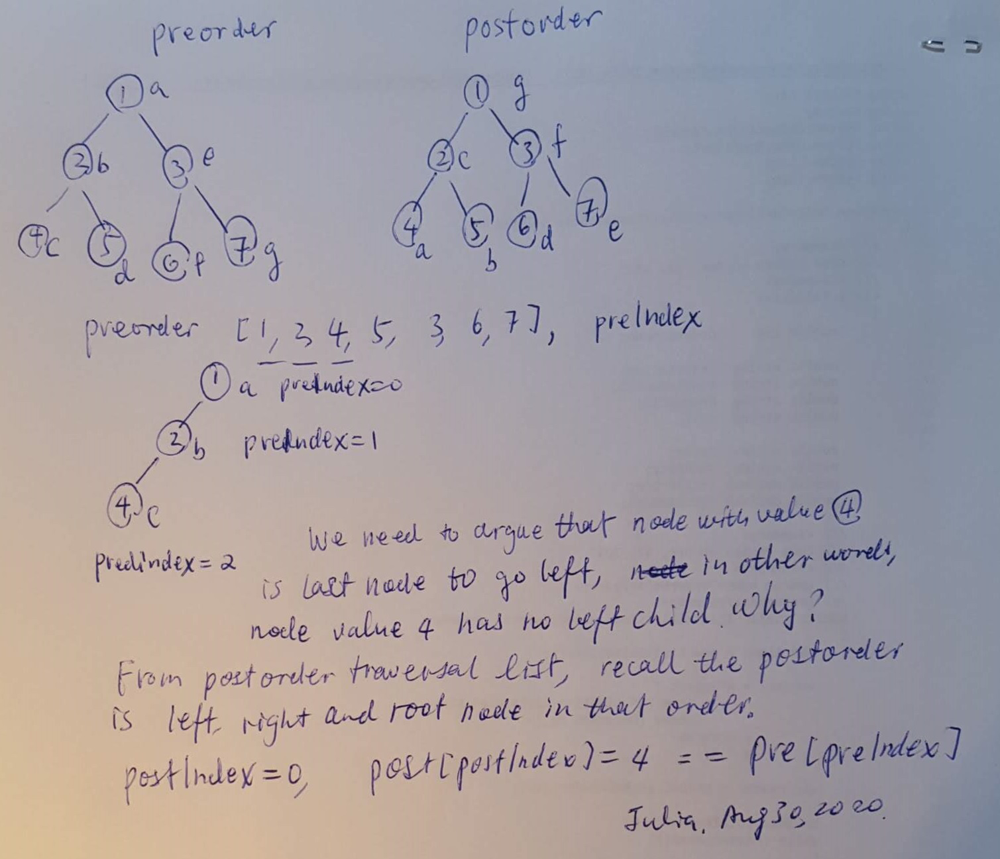
One important task is to argue that when pre[preIndex] == post[postIndex], for example, preIndex = 2, node with value 4 is leaf node, in other words, skip steps to add left and right child.

I think that the idea is hard to figure out and I will come back later to see if I can learn better next time.

Design concern
I do think that it is easy to figure out that each time a node is visited in preorder list, the node is added to the binary tree, preIndex variable is incremented by one. And if pre[preIndex] == post[postIndex], then skip to add left or right child, increment postIndex by one.
As long as preIndex and postIndex both have places to increment one, the design is completed. Do not overthink.

Time complexity
It should be O(N).

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    
    public static int preIndex;
    public static int postIndex;
    
    public TreeNode ConstructFromPrePost(int[] pre, int[] post) {   
        preIndex = 0;
        postIndex = 0;
        
        return runPreorder(pre, post);
    }
    
    private TreeNode runPreorder(int[] pre, int[] post)
    {
        var preLength = pre.Length;
        var postLength = post.Length;
        
        if(pre == null || post == null || preIndex >= preLength || postIndex >= postLength)
            return null; 
        
        var rootVal = pre[preIndex];
        
        var root = new TreeNode(pre[preIndex]);
        preIndex++;
        
        if(rootVal != post[postIndex])
        {
            root.left = runPreorder(pre, post);
        }
        
        if(rootVal != post[postIndex])
        {
            root.right = runPreorder(pre, post); 
        }
        
        postIndex++; 
        
        return root;
    }
}