97. Interleaving String

It is a hard level algorithm. I think that it is better for me to spend some time to write a post and share my learning from the algorithm as well. I am planning to write a solution again in next one or two days, just make sure that I can handle edge case properly, and I can handle it in less than 10 to 15 minutes.

Here is my post.

It is challenging to come out dynamic programming solution. One idea is to write down some good thoughts and explain why this one is different from other dynamic programming solution.

Do not memorize the solution

I like to ask the question how to define interleave, why there is no small example in problem statement. I reviewed my own code and was surprised that I did not write down any thought related to interleave. I have to push myself clarify the question first.

Ask clarification questions

I think that we should have a small example to explain how to interleave is accurately defined in problem statement.

s1 = "aa"", s2 ="bb", how to interleave those two string s1 and s2?
The interleave string should keep chars in s1 in original order, chars in s2 in original order. For example, first char can be selected from s1 or s2, both start from index = 0, so it can be 'a' or 'b', and then continue to second char, so it can be two choices from s1 or s2, but it should be first char not visited yet in s1 or s2.

The problem space should be O(N * M), N is s1's length, M is S2's length, so we can build transition state table to solve it from bottom up. If it is not interleaved, then problem space may go up to 2^(N + M) level, it can not be solved using dynamic programming.

Play first and then write the code
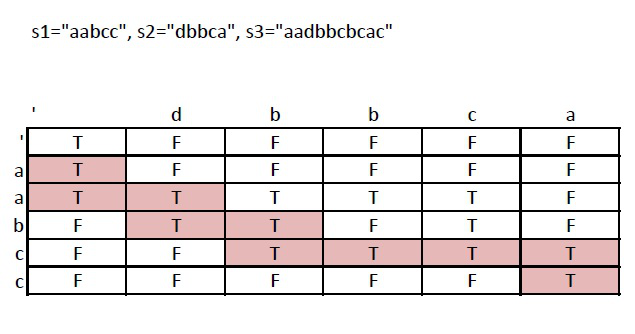
Given s1 = "dbbca", s2 = "aabcc", s3 = "aadbbcbcac", how to solve it using transition table in the following :

subproblems to work on:
s3 = "aa", take the first char from s2, and next char from s2, so it should be true for "aa" and "".
s3 = "aad", take the first two chars from s2, and then first char from s1, so it should be true for "aa" and "d".

I found the second path to the interleave string S3.

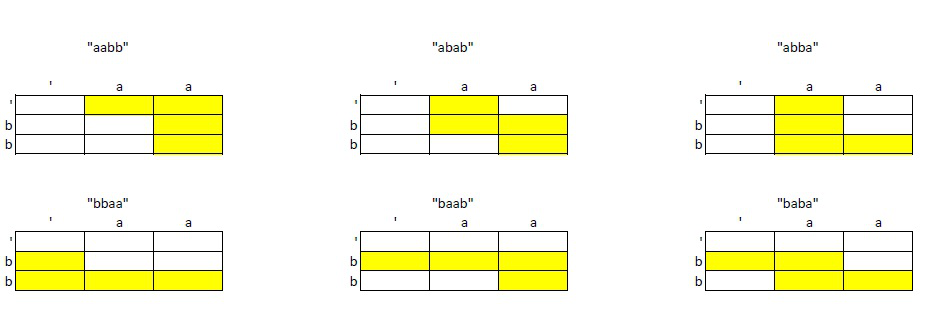
Case study: "aa" and ""bb", interleave "abab"

It is better to work on a small test case, and explain how to approach this problem in general. For example, S1 = "aa", S2 = "bb", then interleave string can have at least 2 * 2 cases by just working on first two chars, "aabb", "abab","baba","bbaa". In total, there are six interleave strings, two more, "abba", "baab".

Work on the matrix, explain how to build a bottom up solution starting from base cases.

Warm up combinatorics

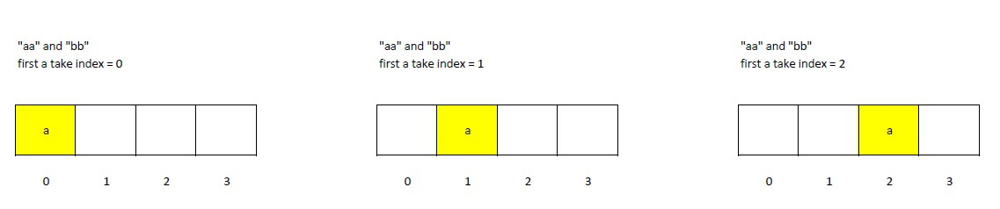
If first 'a' take index = 0, then second 'a' has three choices from index = 1 to 3;
If first 'a' take index = 1, then second 'a' has two choices from index = 2 to 3;
If first 'a' take index = 2, then second 'a' has one choice taking index = 3.
So total choice is 6. The empty two space for "bb", it has to maintain the original order.

This simple example still can be managable. But what if two strings are longer, the brute force solution can be messy. That is the motivation for me to learn dynamic programming and solve the problem without too much detail.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace _97_Interleave_strings
{
    class Program
    {
        static void Main(string[] args)
        {
        }

        /// <summary>
        /// 97 Interleave strings 
        /// Dynamic programming solution
        /// </summary>
        /// <param name="s1"></param>
        /// <param name="s2"></param>
        /// <param name="s3"></param>
        /// <returns></returns>
        public bool IsInterleave(string s1, string s2, string s3)
        {
            if (s1 == null || s2 == null || s3 == null)
                return false;

            var length1 = s1.Length;
            var length2 = s2.Length;
            var length3 = s3.Length;

            if (length3 != length1 + length2)
                return false;

            if (length1 == 0)
                return s2.CompareTo(s3) == 0;

            if (length2 == 0)
                return s1.CompareTo(s3) == 0;

            var rows = length1 + 1;
            var columns = length2 + 1;
            var dp = new bool[rows, columns];

            dp[0, 0] = true;
            // base case: first row
            for (int col = 1; col < columns; col++)
            {
                dp[0, col] = s2[col - 1] == s3[col - 1] && dp[0, col - 1];
            }

            // base case: first column
            for (int row = 1; row < rows; row++)
            {
                dp[row, 0] = s1[row - 1] == s3[row - 1] && dp[row - 1, 0];
            }

            // bottom up - check left and top 
            for (int row = 1; row < rows; row++)
            {
                for (int col = 1; col < columns; col++)
                {
                    var visit1 = s1[row - 1];
                    var visit2 = s2[col - 1];
                    var visit3 = s3[row + col - 1];  // bug: my first writing is row + col - 2

                    // check subproblems - two subproblems, left and top two cases. 
                    dp[row, col] = (visit3 == visit1 && (row - 1 >= 0 && dp[row - 1, col])) ||
                                   (visit3 == visit2 && (col - 1 >= 0 && dp[row, col - 1]));
                }
            }

            return dp[rows - 1, columns - 1];
        }
    }
}