Leetcode discuss: 84. Largest Rectangle in Histogram

Here is my post.

C# review my second practice in August 2018

June 28, 2020

Introduction

I only have two more weeks to prepare Facebook July phone screen. I came cross this algorithm, and I found my practice back in 2018. I found my blogs to document the experience, and I like to write a post to share my learning as well.

January 18, 2018 My blog about Leetcode 84. Here is the blog.
April 10, 2018, here is the blog.
August 5, 2018, here is the blog.

Case study

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
For example, [2, 1, 5, 6, 2, 3]
largest histogram is 5 + 5 = 10

Brute force solution, choose all pair of start and end position, and then calculate the area and keep maximum.

Next, consider how to remove redundant work.
First of all, play with as many simple test cases first, and then try to find ideas to solve the problem.
[3, 2], the answer is 4.
Let us talk about this example, there are three cases to consider, [3], [2, 2], and [2] is skipped since 2 < 3. Make sure that area width 1 and 2 both are considered in comparison.

[5], the answer is 5.
[5, 3], the answer is 6.
[5, 2], the answer is 5.
[1, 5], the answer is 5.

how about [3, 2, 1]?
There are [3], [2, 2], [1, 1, 1], so the maximum one will be 4. First, 3 < 4, so [2, 2]'s area is larger than [3].

[2, 3], the answer is 4.
ascending, how to calculate area and get maximum one is 4.
[2, 3, 4], the answer is to find Math.Max{4, 3 * 2, 2 * 3} = 6. If I enumerate all possible rectangles, three are three areas with one number, two areas with two numbers, one area with three numbers.
We can argue that three areas with one number can be simplified, only check last number since it is largest one.
We also can argue that two areas with two numbers can be simplified, only check last two numbers in ascending order numbers, since rightmost one is largest one.
Based on the test case [2, 3] and [2, 3, 4], we can argue that putting all ascending numbers into stack first, once it goes down, then pop up each number in the stack, and then calculate the maximum one.

test case: [3, 4, 3, 4], maximum area is 12.
How to get the area is 12?
Let me reason one step a time.
First put [3] into stack;
Next 4, 4 > 3, so put 4 into stack; stack: [3, 4];
Next 3, so 3 < peek of top of stack 4, pop 4, calculate area with one number, [4], value should be 4; update max = 4; (why not consider 3? Since 3 < 4, no need to calculate area width 1 with a smaller value, starting from 4.)
continue to compare top of stack, 3 == 3, pop 3, calculate the area with three numbers [3, 4], so the total is 3 * 2 = 6;
Next 4, so put 4 into stack; stack [3, 4];
Now all numbers are visited in the array, pop 4, area is 4 < max = 6;
Pop 3, the stack is empty, in other words, 3 is the minimum number of all numbers in the array, termination case, 3 * length of the array = 3 * 4 = 12, which is bigger than max = 9, so max = 12.

Let me repeat the idea to solve [3, 4, 3, 4]. The idea is to cover all possible areas with different lengths, remove redundant ones if possible. So one of tasks is to find the minimum number in the array, and then area including all numbers span of width will be calculated, the area will be compared with maximum area.

How to find the minimum number of the array? When to remove numbers bigger than minimum number when going through the array iteration one by one?

Breakthrough
Go over test case [3, 4, 3, 4] and explain to myself how to find maximum area 12.
First keep a stack in ascending order, and then first two numbers into stack [3, 4], and the third number is 3, then remove numbers in the stack bigger than 3, and also calculate the area with one number, two numbers, three numbers, ...
Make sure that last number in the stack should be minimum number in the array, all numbers span will be counted to the area with minimum number, which is 12.

In detail, only the following areas are calculated and compared, [4], [3, 4], [4], [3], index value in the stack, so [1], [0, 1], [3], [2], the width calculation is challenge one for special case, last number in the stack.

The following diagram is copied from the blog I wrote in 2018.

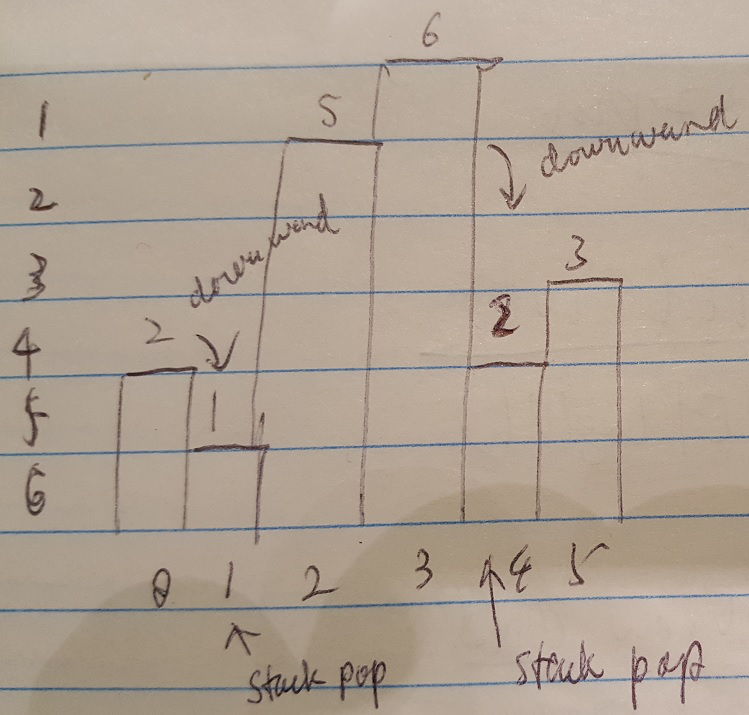
I will write down step by step how to work on the example, calculate the area of largest rectangle in the histogram.

I will add more review later. Stay tuned.

Problems in my practice back in 2018
I do not understand the power of case study. I need to write down a challenge test case, and then step by step explain to myself how to solve the problem? How to improve using stack data structure? What is most challenging part in the design.

I do think that [3, 4, 3, 4] is a good test case for me to remember to solve the problem. Go over the steps to find maximum area 12.

public class Solution {
    public int LargestRectangleArea(int[] height) {
            var stack = new Stack<int>();

            var index = 0;
            var largestArea = 0;

            int length = height.Length; // 6

            while (index < length) // true; index = 1; index = 2;
            { 
                //     stack empty            going upward
                if (stack.Count == 0 || height[stack.Peek()] < height[index]) // index = 1, false;
                {
                    stack.Push(index++); // 0, index = 1;
                }
                else
                {
                    // going downward and then pop stack, calculate rectangle.
                    popStackAndCalculate(ref largestArea, stack, height, index);
                }
            }

            while (stack.Count > 0)
            {
                popStackAndCalculate(ref largestArea, stack, height, length);
            }

            return largestArea;
        }

        /// <summary>
        /// downward and then pop stack to calculate the rectangle
        /// </summary>
        /// <param name="largestArea"></param>
        /// <param name="stack"></param>
        /// <param name="height"></param>
        private static void popStackAndCalculate(ref int largestArea, Stack<int> stack, int[] height, int rightIndex)
        {
            int length = height.Length; // 6

            int lastHeight = height[stack.Pop()]; // 2
            int width = stack.Count == 0 ? rightIndex : rightIndex - stack.Peek() - 1; // 1

            largestArea = Math.Max(largestArea, lastHeight * width); // 2 * 1
        }
}